Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка

(2.1)

Интегральные кривые в этом случае имеют вид:

(2.2)

(2.3)

Найдем состояния равновесия системы (2.1). Приравняв правые части системы нулю и исключив переменную y, получим следующее уравнение для определения абсцисс состояний равновесия:

(2.4)

Из (2.4) получаем, что

, , , .

Ординаты точек покоя имеют вид:

, , , .

Итак, имеем точки

, , , .

Исследуем поведение траекторий в окрестностях состояний равновесия , , , .

Исследуем точку .

Составим характеристическое уравнение в точке .

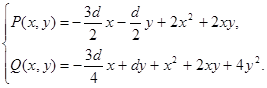
Отсюда

(2.5)

Следовательно, характеристическое уравнение примет вид:

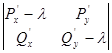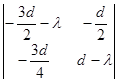==0.

,

Или

.

Характеристическими числами для точки системы (2.1) будут

.

Корни - действительные, различных знаков не зависимо от параметра d. Следовательно, точка - седло.