Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка

.

Составим характеристическое уравнение в точке

.

Согласно

равенствам (2.5) характеристическое уравнение примет вид:

,

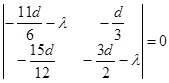
Или

.

Характеристическими числами для точки системы (2.1) будут

,

то есть

, .

Корни - действительные и одного знака, зависящие от параметра d. Если d<0, то точка

-

неустойчивый узел, если d>0, то точка

-

устойчивый узел.

Исследуем точку .

Применяя равенства (2.5), составим характеристическое уравнение в точке

:

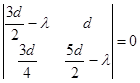
Характеристическими числами для точки

системы (2.1) будут

,

то есть

, .