Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка

Характеристическими числами для точки системы (2.8) будут

, .

Корни - действительные и одного знака, зависящие от параметра d. Если d<0, то точка - неустойчивый узел, а если d>0, то точка - устойчивый узел.

3. Исследуем поведение траекторий в окрестности точки .

Составим характеристическое уравнение согласно (2.11)

.

Характеристическими числами для точки системы (2.8) будут

,

Корни - действительные и одного знака, зависящие от параметра d. Если d<0, то точка - устойчивый узел, если d>0, то точка - неустойчивый узел.

4. Исследуем поведение траекторий в окрестности точки .

Согласно (2.11) составим характеристическое уравнение:

Характеристическими числами для точки системы (2.8) будут

,

Корни - действительные и разных знаков не зависимо от параметра d, следовательно - седло.

Исследуем бесконечно - удаленную часть плоскости системы (2.8) вне концов оси oy. Преобразование [7] переводит систему (2.8) в систему:

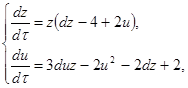(2.12)

где .

Изучим бесконечно - удаленные точки на оси U, то есть при z=0. Получаем:

Следовательно .

Таким образом, получаем две точки N₁ (0,-1) и N₂ (0,1), которые являются состоянием равновесия. Исследуем характер этих точек обычным способом.

Составим характеристическое уравнение в точке N₁ (0,-1).

(2.13)