Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго порядка

Имеем:

, .

Корни -действительные и различные по знаку, следовательно точка N₁ (0,-1) - седло.

Исследуем точку N₂ (0,1).

Согласно (2.13) составим характеристическое уравнение:

, .

Корни -действительные и одного знака, значит точка N₂ (0,1) - устойчивый узел.

Исследуем концы оси y с помощью преобразования [7] . Это преобразование переводит систему (2.8) в систему:

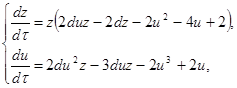(2.14)

где .

Для исследования состояний равновесия на концах оси y, нам необходимо исследовать только точку N₃ (0,0). Составим характеристическое уравнение в точке N₃ (0,0):

Корни - действительные и одного знака, значит точка N₃ (0,0) - неустойчивый узел.

Теперь дадим распределение состояний равновесия системы (2.1) в виде таблицы 2.

Таблица 2.

d					∞
					N1	N2	N3
(-∞; 0)	седло	неуст. узел	уст. узел	седло	седло	уст. узел	неуст. узел
(0; +∞)	седло	уст. узел	неуст. узел	седло	седло	уст. узел	неуст. узел

Положение кривых (2.9), (2.10) и расположение относительно их состояний равновесия при d<0 и d>0 дается соответственно рис.2 (а, б).

Поведение траекторий системы в целом при d<0 и d>0 дается рис.5 (а, б) приложения Б: Поведение траекторий системы (2.8).

Вопрос о существовании предельных циклов не возникает, так как Воробьев А.П. [5] доказал, для квадратичной системы предельный цикл не может окружать узел.

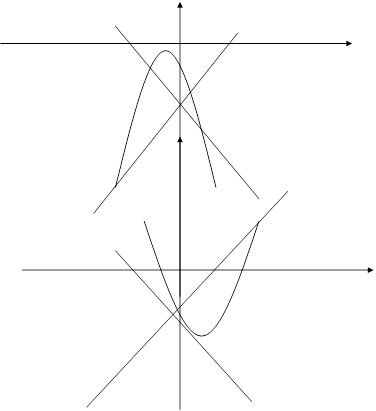
а (d<0) б (d>0)

Рис. 2

2.3 Исследование системы (1.1) с коэффициентами, заданными формулами (1.52) - (1.53)

Будем проводить наше исследование в предположении, что

, .

Пусть мы имеем систему (1.1), коэффициенты которой определяются формулами (1.52) - (1.53). Тогда система (1.1) будет иметь вид:

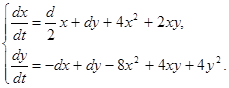(2.15)

Интегральные кривые в этом случае имеют вид: