Дипломная работа: Комплексные числа избранные задачи

Степени мнимой единицы.

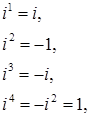
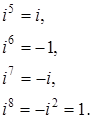
Если натуральный показатель степени m при делении на 4 дает в остатке r, т.е. если , где n – натуральное число, то

;

при этом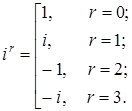

Комплексное число называется сопряженным комплексному числу , если

.

Свойства операции сопряжения.

1.

2. Для любого действительного числа a справедливо равенство

3. Для любого действительного числа b справедливо равенство

4.

5.

Следствие из 5.

6.

7. Сумма и произведение двух комплексно сопряженных чисел являются действительными числами.

Следствие из 7.

Модулем комплексного числа называется действительное число вида

.

8. Теорема о сопряженном корне.

Если число является корнем уравнения

(1)

с действительным коэффициентами a0 , a1 , …, an , то число также является корнем уравнения (1).

Извлечение квадратного корня из комплексного числа . Пусть

,

где x и y– действительные числа. Возводя обе части этого равенства в квадрат, получаем

.