Дипломная работа: Комплексные числа избранные задачи

2) . Тогда система равносильна системе , которая имеет два решения: и .

Итак, искомых чисел четыре: ; ; , из них два числа и – действительные, а два других и – комплексно сопряженные.

Ответ: ; ; .

Задача 21. Известно, что , . Найдите:

а) ; б) .

Решение

а) ,

б) .

Ответ: а) ; б) .

Задача 22. При каких действительных значениях x и y комплексные числа и будут сопряженными?

Решение

Комплексные числа и будут ком-

плексно сопряженными, если выполняются условия:

Ответ: ; .

Задача 23. Докажите тождество .

Решение

Пусть , , . Тогда , ,, ,,.

Отсюда легко следует доказываемое тождество.

Задача 24. Докажите, что если число является чисто мнимым, то .

Решение

По условию , где b – действительное число, тогда , , .

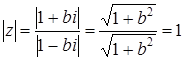Тождество доказано.

Задача 25. Пусть . Докажите, что .

Решение

Поскольку , то