Дипломная работа: Комплексные числа избранные задачи
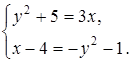
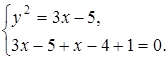
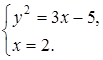
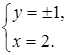
Ответ: 
; 
.
Задача 5. При каких действительных значениях x и y комплексные числа 
и 
будут равными?
Решение
Комплексные числа 
и 
будут равными, если выполняются условия:
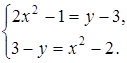
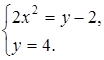
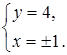
Ответ: 
; 
.
Задача 6. Решите уравнение 
относительно действительных переменных x и y.
Решение
Левую часть уравнения можно рассматривать, как некоторое неизвестное комплексное число. Приведя его к виду 
, получаем уравнение равносильное данному: 
. Так как два комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, приходим к системе:
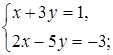
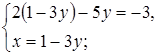
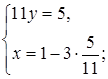
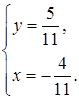
Ответ: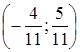 
.
Задача 7. Решите во множестве комплексных чисел уравнение 
.
Решение
Так как 
, тогда корни находятся по формуле
(
).
Отсюда, 
, 
.
Ответ: 
.
Задача 8. Решите уравнение 
.
Решение
Перепишем уравнение в виде 
.
Полагая 
, получим уравнение 
, которое имеет корень 
. Поэтому левую часть этого уравнения можно представить в виде произведения двучлена 
и квадратного трехчлена.
Для нахождения коэффициентов квадратного трехчлена применим схему Горнера:
| 1 | 1 | 2 | – 4 | |
| 1 | 1 | 2 | 4 | 0 |
Итак, получаем уравнение 
.
Квадратный трехчлен 
имеет корни 
и 
.
Следовательно, исходное уравнение имеет корни: 
, 
, 
.
Ответ:
; .
Задача 9. Решите уравнение 
.
Решение