Дипломная работа: Комплексные числа избранные задачи

Задача 26. Решите уравнение .

Решение

Пусть . Тогда данное уравнение запишется в виде , откуда . Комплексное число равно нулю, тогда и только тогда, когда его действительная и мнимая части равны нулю; поэтому для нахождения неизвестных x и y получим систему:

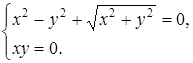
Из второго уравнения этой системы находим: x=0 и y=0. При x=0 первое уравнение системы запишется в виде или . Отсюда находим или . Таким образом, числа , , являются решениями данного уравнения.

При y=0 для нахождения x получаем уравнение . Отсюда следует, что x=0, и тем самым .

Ответ: ; ; .

Задача 27. Решить систему уравнений:

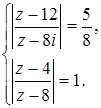
Решение

Полагая , имеем

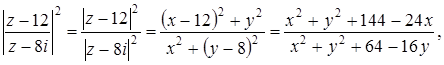
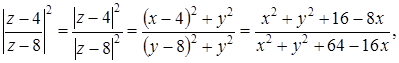
следовательно, 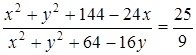и .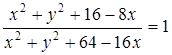

После преобразований данная система принимает вид

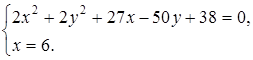
Решение полученной системы является пары и . Таким образом, исходная система имеет два решения и .

Ответ: ; .

Задача 28. Докажите, что если , то .

Решение

Предположим, что существует такое комплексное число , , для которого выполнено неравенство . Тогда , или .

Поскольку

то и – действительные числа. Поэтому из последнего неравенства получим неравенство: .

Следовательно, .