Дипломная работа: Комплексные числа избранные задачи

Второй корень уравнения является числом, сопряженным с данным корнем , то есть . По теореме Виета находим

; ,

где число 2 – это второй коэффициент уравнения, взятый с противоположным знаком, а число 5 – свободный член. Таким образом, получаем уравнение

.

Ответ: .

Задача 18. Даны числа ; . Найдите:

а); б) .

Решение

а) , тогда

б) , тогда

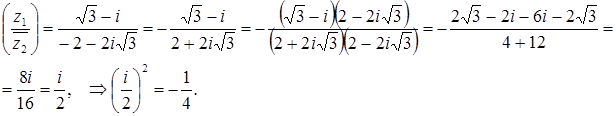Ответ: а) ; б) .

Задача 19. Зная, что корнем уравнения является число , найдите все корни данного уравнения.

Решение

Поскольку все коэффициенты данного уравнения – действительные числа, то на основании теоремы о сопряженном корне, делаем вывод, что число также является корнем данного уравнения.

Пусть – неизвестный корень уравнения , тогда , где

, получаем .

Разделим обе части последнего равенства на , получим .

Следовательно, .

Ответ: ; .

Задача 20. Найдите все комплексные числа, каждое из которых сопряжено со своим квадратом.

Решение

Пусть – искомое комплексное число, где x и y – действительные числа. Тогда число , сопряженное числу , равно .

По условию задачи имеем: , т.е. .

Преобразовав это уравнение, получим: .

Два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Следовательно, последнее уравнение равносильно следующей системе уравнений с действительными переменными x и y:

Возможны два случая:

1) . Тогда система равносильна системе: , которая