Большое распространение при анализе технологических задач обработке давлением находит метод конечных элементов (МКЭ) [6,15,16,41,42], который относится к современным методам численного анализа. Первое его применение связано с расчетом инженерных конструкций. Начиная с этого первого применения, МКЭ в течение короткого времени развился в самостоятельную область науки, получившую широкое распространение в решение граничных задач математики, физики и особенно механики сплошной среды. Быстрое развитие МКЭ шло наряду с прогрессом компьютерной техники и ее применением в различных областях науки и инженерной практики.

Метод конечных элементов включает различные подходы, в которых для определения напряжения, деформации и перемещения материал условно разбивают на отдельные элементы, соединенные в узловых точках. Применение этого метода может успешно проводиться как для жесткопластического материала, так и для упругопластического. Этот выбор, также как и выбор конечного элемента, осуществляется, исходя из постановки задачи и рациональности использования того или иного подхода, описанного в МКЭ. Задание граничных условий и введение некоторых гипотез позволяет в значительной степени упростить поиск решения, хотя и в некоторой степени усредняет результат. Однако следует заметить, что для части процессов МКЭ может являться единственным методом, позволяющим достигать необходимого результата с достаточной степенью точности.

В качестве наиболее весомых преимуществ МКЭ можно привести следующие:

· Свойства материалов смежных элементов не должны быть обязательно одинаковыми. Это позволяет применять метод к телам, состоящим из нескольких материалов.

· Криволинейная область может быть аппроксимирована с помощью прямолинейных элементов, или описана точно с помощью криволинейных элементов.

· Размеры элементов могут быть переменными. Это позволяет укрупнить или измельчить сеть разбивки области на элементы, если в этом есть необходимость.

· С помощью МКЭ не представляет труда рассмотреть граничные условия с разрывной поверхностной нагрузкой, а также смешанных граничных условий.

Указанные выше преимущества МКЭ могут быть использованы при составлении достаточно общей программы для решения частных задач определенного класса.

Одной из основных задач при использовании конечно-элементного анализа является построение сетки конечного элемента. С целью упрощения подготовки и проверки входных данных применяется автоматическое построение сетки, что стало возможным благодаря достаточно высокой степени развития компьютерной техники и прикладного программного обеспечения [18]. Кроме того, автоматизация позволяет уменьшить ошибки операторов, обеспечить регулярность сетки, облегчить использование других типов элементов, упростить параметрические исследования.

1.5 Выводы

Обзор работ, посвященных осадке кольцевых заготовок показал:

1. Осадка является эффективным методом обработки металлов давлением, позволяющим значительно экономить материал.

2. Основным дефектом осадки кольцевых заготовок является потеря устойчивости, вследствие тонкостенности заготовки.

3. Теоретические исследования процесса в основном посвящены оценке силовых режимов и не отражают реальную картину течения материала.

4. Недостаточно уделено внимание напряженно-деформированному состоянию осаженной заготовки.

5. Метод конечных элементов является наиболее универсальным и приемлемым методом решения технологических задач.

1.6 Цель работы и задачи исследования

Целью работы является создание математической конечно-элементной модели осадки кольцевой заготовки, описывающей механизм осаживания заготовки между плоскими шероховатыми плитами, позволяющей прогнозировать устойчивость заготовки.

Задачи исследования:

- создать математическую модель процесса осадки кольцевых заготовок с учетом реальных свойств материала;

- провести исследования напряженно-деформированного состояний заготовки, кинематики течения материала при различном состояние заготовки;

- создание программного обеспечения математического моделирования процесса осадки кольцевых заготовок.

2. Основные соотношения конечно-элементного анализа процессов упруго-пластического деформирования

2.1 Вариационные подходы к решению задач методом конечного элемента

Основная идея МКЭ основывается на замене некоторой непрерывной величины в пределах рассматриваемой области дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами (КЭ). Неизвестная искомая величина в пределах каждого КЭ аппроксимируется, как правило, полиномиальной функцией заданного вида с учетом требования непрерывности на границах смежных КЭ. При этом выбор формы конечного элемента и вида выражения, аппроксимирующего действительный закон изменения исследуемой величины в пределах КЭ, является одним из наиболее ответственных моментов в общей процедуре МКЭ, от которого существенно зависит точность приближенного решения. Таким образом, непрерывная в пределах исследуемой области неизвестная величина (например, перемещение, скорость перемещения, напряжение, температура и т. д.) представляется через конечное число ее дискретных значений в узлах элементов[15,41,42].

Построение разрешающих уравнений МКЭ для решения задач механики деформируемых сред базируется на соответствующих вариационных принципах и вытекает из оптимизации некоторой интегральной величины (функционала), связанной с работой или мощностью напряжений и внешней приложенной нагрузки при соблюдении заданных граничных условий. В общем виде такой функционал с учетом действия массовых и поверхностных сил можно представить выражением:

(2.1)

где N_Д - работа или мощность внутренних сил;

N_М - работа или мощность, развиваемая массовыми силами,

N_В - работа или мощность внешних сил.

Дальнейшая процедура МКЭ предусматривает представление выражения (2.1) в виде функционала значений неизвестных только в узлах КЭ и построение разрешающей системы уравнений путем минимизации J по всем узловым переменным:

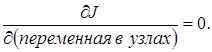(2.2)

Однако, указанный способ получения разрешающих уравнений для КЭ с помощью функционала (2.1) не является единственно возможным. В настоящее время уравнения для элементов получают путем минимизации функционала, связанного с рассматриваемым дифференциальным уравнением соответствующей задачи математической физики. Известны также конечно-элементные решения, основанные на методе Галеркина. В последнем случае отпадает необходимость в вариационной формулировке задачи.