Дипломная работа: Обратимые матрицы над кольцом целых чисел
Квадратная матрица, у которой все элементы, за исключением элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается Е. :
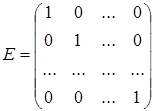
Две матрицы считаются равными, если они одного размера и у них совпадают соответствующие элементы.
Две матрицыA =(a ij ) и B =(b ij ) одного и того же размера ![]() можно складывать, их суммой будет матрица того же размера C =(c i j ),
можно складывать, их суммой будет матрица того же размера C =(c i j ), ![]() , т.е. чтобы получить сумму двух матрицы достаточно сложить соответственные элементы этих матриц.
, т.е. чтобы получить сумму двух матрицы достаточно сложить соответственные элементы этих матриц.
Произведение элемента c из поля на матрицу A =(a ij ) определяется следующим образом: cA = (caij ).
Для любой матрицы A существует противоположная - A такая, что
A + (- A )=0 .
Все перечисленные свойства непосредственно следуют из определений и свойств операций в поле.
Рассмотрим матрицу A =(a ij ) размером ![]() и матрицу B =(b ij ) размером
и матрицу B =(b ij ) размером ![]() (т.к. произведение матриц определено лишь в том случае, когда число столбцов в первой матрице равно числу строк во второй). Для таких матриц введем действие умножения матрицы на матрицу, в результате чего получается матрица C = (cij ) размером
(т.к. произведение матриц определено лишь в том случае, когда число столбцов в первой матрице равно числу строк во второй). Для таких матриц введем действие умножения матрицы на матрицу, в результате чего получается матрица C = (cij ) размером ![]() , где
, где  .
.
Итак, матрицы можно складывать, умножать их на скаляр, а также умножать матрицу на матрицу. Эти действия обладают свойствами:
По сложению:
1. (A + B )+ C = A + (B + C ) – ассоциативность;
2. A + B = B + A – коммутативность;
3. Существует нейтральный элемент – матрица 0: A + 0 = 0 + A = A ;
4. Для матрицы A существует обратный элемент - A : A + (- A )=0 ;
По умножению матриц на скаляр:
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ;
;
8. ![]() ;
;
По умножению матриц:
9. Произведение матриц в общем случае не коммутативно, т.е. AB![]() ВА ;
ВА ;
10. (AB )C = A (BC ) – ассоциативность;
11. (cA )B = A (cB )= cAB ;
12. Дистрибутивность умножения относительно сложения (правая и левая)(A 1 + A 2 )B = A 1 B + A 2 B , A (B 1 + B 2 )= AB 1 + AB 2 ;
13. Существует единственный нейтральный элемент E
(если A – квадратная): EA = AE = A . Если же A размером ![]() , то
, то
Em A = AEn = A .
14. Произведение матрицы А на нулевую матрицу дает в результате так же нулевую матрицу (существуют случаи, когда нулевая матрица получается в результате перемножения ненулевых матриц).
Для квадратных матриц фиксированного порядка n действия сложения и умножения определены всегда, и их результатами являются квадратные матрицы того же порядка. Таким образом, квадратные матрицы фиксированного порядка образуют кольцо.
Определителем n -го порядка квадратной матрицы А , называется алгебраическая сумма n ! членов, которыми являются всевозможные произведения по n элементов, взятых по одному и только по одному из каждой строки и каждого столбца, причем член берется со знаком плюс, если его индексы составляют четную перестановку, и со знаком минус – если нечетную перестановку.
![]()
 ,
,
где (a 1 , a 2 , ..., a n ) пробегает все перестановки чисел 1, 2, ..., n ; множитель ![]() равен +1, если (a 1 , a 2 , ..., a n ) - четная перестановка, и равен –1, если нечетная.
равен +1, если (a 1 , a 2 , ..., a n ) - четная перестановка, и равен –1, если нечетная.