Дипломная работа: Обратимые матрицы над кольцом целых чисел

Министерство образования Российской Федерации

Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Обратимые матрицы над кольцом Z_n

Выполнила:

Студентка V курса

Математического факультета

Сычева О. Г.

Научный руководитель:

д.ф.-м.н., профессор

Вечтомов Е. М.

Рецензент:

к.ф.-м.н., доцент

Чермных В. В.

Допущена к защите в ГАК

???.???????? ???????? ? ?.
? ?
????? ?????????? ????????? ?. ?.
? ?

Киров 2003

Содержание:

Введение………………………………………….…………………….2 стр.

§1 Основные понятия………………………………………………….3 стр.

§2 Обратимые матрицы над полем Z_p

п.1 формула для подсчета обратимых матриц порядка 2 ……….10 стр.

п.2 формула для подсчета обратимых матриц порядка 3 ……….11 стр.

п.3 общая формула подсчета обратимых матриц над полем Z_p ..16 стр.

§3 Обратимые матрицы над Z _n ………………………………………17 стр.

Литература …………………………………………………………….27 стр.

Введение

Теория матриц является одним из основных вопросов линейной алгебры.

Цель данной работы: подсчитать количество обратимых матриц над кольцом вычетов и по возможности получить формулу для их вычисления. Для вычисления количества обратимых матриц воспользовались теорией определителей и полным перебором всех возможных вариантов получения элементов в кольцах вычетов.

Вся работа разбита на два этапа:

В §2 показан метод построения обратимых матриц второго и третьего порядков над полем Z_p . В конце параграфа построена гипотеза формулы подсчета количества обратимых матриц n–го порядка над полем Z_p .

В §3 приведен алгоритм построения обратимых матриц второго порядка над некоторыми кольцами вычетов (приведены конкретные примеры). В конце параграфа построена гипотеза формулы подсчета количества обратимых матриц второго порядка над кольцом классов вычетов Z _n .

§1. Основные определения.

Матрицей называется прямоугольная таблица, заполненная некоторыми математическими объектами. Чаще всего рассматриваются матрицы, заполненные элементами из некоторого поля P .

Элементы матрицы обозначаются одной буквой с двумя индексами, указывающими "адрес" элемента - первый индекс дает номер строки, содержащий элемент, второй - номер столбца. Если матрица имеет m строк и n столбцов, то говорят, что матрица имеет размерность (или - размеров ). Мы будем обозначать матрицы заглавными латинскими буквами, а ее элементы - такими же буквами, но строчными. Таким образом, матрица (размеров ) записывается в форме:

.

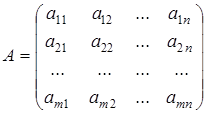Матрица, состоящая из одних нулей, называется нулевой.
Будем обозначать ее 0 .

Матрица, имеющая одно и то же число n строк и столбцов, называется квадратной. Число n называется порядком квадратной матрицы.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--