Дипломная работа: Обратимые матрицы над кольцом целых чисел

Формулу выведем в 2 этапа.

1) Пусть (р-1 штук), (р-1 штук),

(по р штук) (1.2) .

Тогда количество матриц, удовлетворяющих данным условиям, вычисляется по формуле

(р-1)² р² (1.3)

Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что , .

В условии (1.2) не учитываются матрицы вида с неравным нулю определителем, количество которых нужно прибавить.
Но сосчитали матрицы вида с определителем обращающимся в нуль, количество которых нужно вычесть.

Докажем, что количество матриц в обоих случаях одинаково.

а) (р-1 штук), и . Из (1.1) получаем равенство . Значит . При заданном (где =1,2…р-1) элемент однозначно выражается через и (количество невырожденных матриц – р-1). Поэтому количество матриц удовлетворяющих этим условиям (р-1)³ штук.

б) , и . Значит . Отсюда . Элемент однозначно выражается через , , , которые принимаю не нулевые значения. Поэтому количество матриц удовлетворяющих этим условиям (р-1)³ штук

Значит формула (1.3) при условии (1.2) верна.

2) Пусть . Тогда , а из (1.1) получаем что и (как в первом этапе, случае а). Тогда количество таких матриц вычисляется по формуле

(р-1)² ×р (1.4)

Этими этапами мы перебрали все случаи невырожденных матриц.

Складывая формулы (1.3) и (1.4) полученные в этапах 1) и 2) получаем формулу для нахождения количества обратимых матриц порядка 2 над полем Z_p

(р-1)² ×р×(р+1) (1.5)

2. Формула для подсчета обратимых матриц порядка 3.

Будем рассматривать матрицы .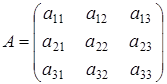

Алгебраические дополнения к элементам , и есть определители матриц , и соответственно, порядка 2, при чем 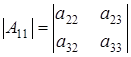, 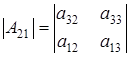и .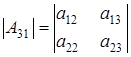

Нужно найти количество всех невырожденных матриц ().
При этом

(2.1)

Формулу выведем в 3 этапа.

1) Пусть (р-1 штук), (их количество по формуле (1.5) ), (по р штук) (2.2) .

Тогда количество таких матриц вычисляется по формуле

(р-1)³ р⁵ (р+1) (2.3)

Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что , .

При условии (2.2) не учитываются матрицы вида 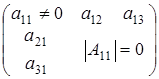с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида 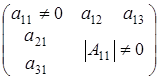с определителем обращающимся в нуль, количество которых нужно вычесть.

Докажем, что количество матриц в обоих случаях одинаково:

а) (р-1 штук), и . Из (2.1) получаем равенство .

а1) Пусть =0. Тогда и. Значит элементов всего р-1 штук, количество невырожденных матриц - (р-1)² р(р+1). Т.к то из выражения получаем равенство , т.е. хотя бы один из этих элементов не равен нулю. Пусть . Из того, что получаем .Элементом , принимающим любое значение, можем однозначно задать элемент . Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁴ ×р² ×(р+1) штук.

а2) Если ¹0, .Тогда и . Значит элементов всего р-1 штук, количество невырожденных матриц - (р-1)² р(р+1). Т.к , то, из выражения получаем . Пусть . Домножим равенство () на . Заменим на (из того, что ). Получим равенство . Вынесем за скобки и т.к. делаем вывод, что . Значит и (). Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁵ ×р×(р+1) штук.

а3) Если ¹0, и получаем (р-1)⁴ ×р² ×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1)

а4) Если ¹0, , и получаем
(р-1)⁵ ×р×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а2)

а5) Если ¹0, , и . Из того, что получаем . Пусть . Равенство () умножим на и заменим на (). Получим равенство . Вынося за скобки (), замечаем, что элемент однозначно выражается через ( - р-1 штук). Но тогда тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)⁶ ×р×(р+1)штук.

Таким образом, общее количество матриц удовлетворяющих условию пункта а) подсчитывается по формуле
(р-1)⁴ ×р×(р+1)×(р² +2р-1) (получается суммированием формул полученных в пунктах а1-а5).