Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

В своей работе Renyi исследовал одномерную задачу о случайном заполнении пространства автостоянки, точнее ряда парковочных мест. Процедура состоит в последовательном расположении автомобилей на отрезке случайным образом. Интервал заполняется некоторыми одинаковыми отрезками (автомобилями), условно равными по величине 1 и не имеющими общих точек, то есть не пересекающимися. В итоге решения задачи делается вывод о том, что при достаточно больших эти отрезки заполняют интервал на 74,8%. Число отрезков - случайная величина.

Авторы исследуют асимптотическое поведение моментов величины . Доказывается, что величина (нормированная величина ) имеет асимптотически нормальное распределение с параметрами при .

1.2 Описание предметной области и постановка задачи

Рассмотрим случайный процесс, в котором автомобили длиной «1» паркуются на отрезке где . Первый автомобиль размещается так, что положение его центра – случайная переменная, имеющая равномерное распределение на отрезке .

, (a=1)

Если остается пространство для размещения второго автомобиля, то он паркуется так, что его центр – случайная величина, распределенная на отрезке , с расстоянием от первого автомобиля.

Если на данном отрезке парковки остается пустой промежуток длины , то паркуется третий автомобиль. Его центр – случайная величина, распределенная равномерно, расстояние до разместившихся машин и так далее до конца отрезка, возможного для парковки.

Обозначим через число машин, занявших место на стоянке. Тогда для и определено для всех .

Выводы по главе

-задача парковки сводится к исследованию распределения целочисленной случайной величины при ;

-итогом решения задачи является то, что при достаточно больших автомобили заполняют интервал на 74,8%.

2. Математические методы решения задачи парковки

2.1 Решение задачи парковки

A. Renyiв работе [1] доказал, что математическое ожидание .

удовлетворяет соотношению (2.1.1)

где постоянная 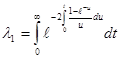, (2.1.2)

В работе [2] соотношение (2.1.1) 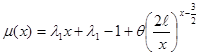(2.1.3)

и доказано, что среднее квадратическое отклонение

удовлетворяет соотношению (2.1.4)

где - некоторая постоянная величина.

Кроме того, доказано, что стандартная случайная величина

имеет предельное нормальное распределение с параметрами от (0,1) при .

Доказывается двумя способами:

а) все моменты сходятся к нормальным моментам при ;

б) непосредственное применение центральной предельной теоремы для сумм независимых случайных величин.

а) нормальное распределение:

плотность вероятности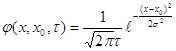

функция распределения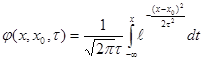

б) центральная предельная теорема:

Если , … - независимо одинаково распределенные случайные величины, и имеющие математическое ожидание и дисперсию , то при закон распределения суммы : неограниченно приближается к нормальному [6]:

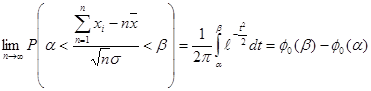
Для решения задачи парковки рассматриваются некоторые интегральные уравнения.

Пусть для интервал будет случайным интервалом, занятым первой машиной, вставшей на стоянку на отрезке длины . Процесс парковки таков, что число машин, которые будут в конце концов размещены от первой, не зависят от числа машин, которые уже размещены на стоянке. При этом число машин, размещенных на отрезке , имеют распределение , а число машин на отрезке имеют распределение . Следовательно, условное распределение , при условии, что первая машина занимает такое же, как распределение , где и независимы, тогда