Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

таким образом при

Находим

начальные условия на интервале

Подставим в решение начальные условия для определения :

таким образом на интервале .

Дальнейшее интегрирование сложно.

Используя независимость и для функции

(2.1.14)

получаем соотношение (2.1.15)

Так как , (2.1.16)

то из выражения (2.1.15) следует, что (2.1.17)

Пусть (2.1.18)

где , найдем для

(2.1.19)

так как (2.1.20)

то (2.1.21)

интегрируя, получим: 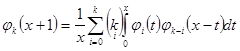(2.1.22)

2.2 Некоторые сведения из теории вероятности, использованные для решения задачи парковки

Соотношение (2.1.3): 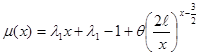и соотношение (2.1.4):

получены при использовании теорем.

Теорема 1: пусть определена для и удовлетворяет

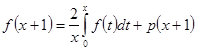при (2.2.1) [6]

где - непрерывна для и такая, что если (2.2.2)