Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

Так как равномерно распределено на , то (2.1.6)

и для выполняется интегральное уравнение:

парковка автостоянка математический оптимизация

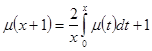, (2.1.7)

Введем функцию (2.1.8)

Для можно записать более простое интегральное уравнение:

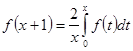
(2.1.9)

Начальные условия: при и (2.1.10)

тогда можно определить последовательно на интервалах , ,...

Вычислим на интервале :

запишем уравнение (2.1.9) в виде: 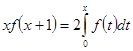(2.1.11)

Продифференцируем по : (2.1.12)

сделаем замену: ,

получим:

Рассмотрим решение на интервале с начальным условием :

(2.13)

Находим :

тогда

таким образом на интервале .

Аналогично находим на интервале с начальными условиями: , , ;

на интервале с начальными условиями: , , .

Интервал :

находим , учитывая начальные условия: при