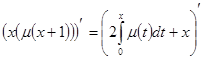Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

(2.3.12)

где - произвольная постоянная, определенная из начальных условии.

Вернемся к исходному уравнению:

(2.3.13)

где , где - искомая функция.

Умножим обе части уравнения на и проинтегрируем по от до :

(2.3.14)

из сравнения (3.12) и (3.14) получаем:

при этом , где (2.3.15)

- постоянная величина (вычислена Simon Sandor).

Рассмотрим исходное уравнение:

разделим обе части его на и перейдем к пределу при

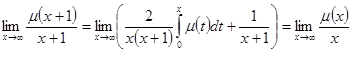
Следовательно, 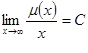, где 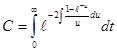(2.3.16)

из условия и условия 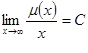можно получить (2.3.17)

Так как , то , следовательно, функция - возрастающая, притом монотонно при .

Умножим исходное уравнение на и дважды продифференцируем: