Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы
тогда существует ![]() , такая, что полагая
, такая, что полагая
![]()
![]() (2.2.3)
(2.2.3)
получим![]()
![]() (2.2.4)
(2.2.4)
Следствие: если ![]() и
и ![]() удовлетворяет условию (2.2.1) с
удовлетворяет условию (2.2.1) с
![]()
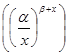 (2.2.5),
(2.2.5),
то ![]()
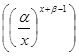 (2.2.6)
(2.2.6)
Теорема 2: пусть ![]() определена для
определена для ![]() и удовлетворяет
и удовлетворяет
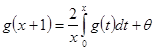
![]() ,
, ![]() где
где ![]() , тогда
, тогда
![]()
![]() (2.2.7) [6]
(2.2.7) [6]
Следствие: пусть ![]() определена для
определена для ![]() и удовлетворяет
и удовлетворяет
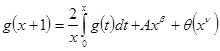
![]() , где
, где ![]() (2.2.8)
(2.2.8)
тогда ![]()
![]() (2.2.9)
(2.2.9)
Эти теоремы [6] применим к проблеме парковки, так как ![]() удовлетворяет уравнению
удовлетворяет уравнению 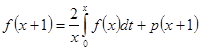
![]() , (учитываем, что
, (учитываем, что 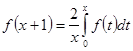 из (2.1.9)), где
из (2.1.9)), где ![]() ,
,
(По теореме 1 ![]() непрерывна для
непрерывна для ![]() и такова, что в предположении
и такова, что в предположении ![]()
![]() , мы имеем
, мы имеем ![]() , тогда существует
, тогда существует ![]() такая, что полагая
такая, что полагая ![]()
![]() имеем
имеем
![]()
![]() )
)
то по теореме 1 получается, что:
![]() (2.2.10)
(2.2.10)
существует, и что для каждого ![]() :
:
![]() (2.2.11).
(2.2.11).
При ![]() из условия
из условия ![]() ,
, ![]() получаем, что
получаем, что
![]() (2.2.12).
(2.2.12).
Так как ![]() и
и ![]() приближаются к
приближаются к ![]() очень быстро, то из (2.2.11) получается хорошая аппроксимация.
очень быстро, то из (2.2.11) получается хорошая аппроксимация.
Так как ![]() для
для ![]() , то грубое приближение
, то грубое приближение ![]() дает
дает
![]() ,
,
следовательно по теореме 1 при условии ![]() следует
следует
Теорема 3: существует постоянная ![]()
![]() такая, что математическое ожидание
такая, что математическое ожидание ![]() величины
величины ![]() удовлетворяет соотношению
удовлетворяет соотношению
![]() (
(![]() ) (2.2.13) [6]
) (2.2.13) [6]
Используя формулу Стирлинга ![]() , получим
, получим
![]()
 (2.2.14)
(2.2.14)
Определим ![]() и
и ![]() :
: ![]()
![]()
![]() , где
, где ![]()