Дипломная работа: Оптимизация расстановки транспортных средств на открытых автостоянках в интересах Государственной противопожарной службы

, () (2.2.15),

учитывая, что - левая часть выражения (2.2.14), следовательно

(2.2.15),

таким образом, удовлетворяет (),

где оценено формулой (2.2.15).

Из этих условии следует

Теорема 4: существует постоянная такая, что дисперсия величины удовлетворяет соотношению [6].

Рассмотрим соотношение: (2.2.16).

Докажем, что случайная величина имеет асимптотически нормальное распределение с параметрами при .

Для доказательства воспользуемся двумя леммами.

Лемма 1: пусть неотрицательная функция, определенная при , ограниченная на конечных интервалах и удовлетворяющая соотношению , тогда при выполняется , где взят по всем наборам неотрицательных , при .

Лемма 2: рассмотрим такое, что для всех - независимых случайных величин, которые удовлетворяют

(2.2.17)

следует, что функция распределения приближается равномерно по к нормальному распределению с нулевым математическим ожиданием и единичной дисперсией.

Пусть фиксированная неотрицательная целочисленная функция от, определенная при и удовлетворяющая условию и .

Рассмотрим первые машин, находящихся на отрезке . Обозначим через расстояние между 0 и самой левой машиной;

- расстояние между этой машиной и машиной, стоящей второй слева и так далее.

- расстояние между машиной, находящейся на правом краю и . Тогда условное распределение , где такое же, как распределение при независимых. Следовательно, условное

распределение равно распределению , где - независимое и определено

По лемме 1, где получаем или

(2.2.18) для каждого .

Отсюда следует для условных дисперсии .

Таким образом верно для для всех достаточно больших и всех случайных . Из условия следует .

Пусть - событие: такое, что , тогда из условия следует, что фиксированного выполняется и при удовлетворяет условию .

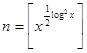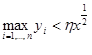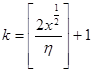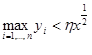Определим функцию , положив и обозначим событие: . Возьмем и разделим отрезок на интервалов одинаковой длины, обозначенных , тогда, если условие неверно, принимается, что, по крайней мере, один из интервалов разбивается по первым припаркованным на стоянку машинам.

Вероятность, это меньше, чем 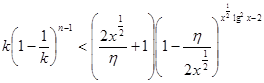и , при [5]. Следовательно, .