Дипломная работа: Показательно-степенные уравнения и неравенства

При

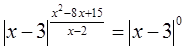
2) , и . - решение, а .

3) для всех . При и все решения содержатся в уравнении , или . При , .

При , - верно. .

Ответ: 4, 5.

Пример №15.

,

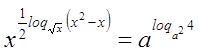Решение

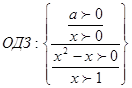
используя свойства логарифма и получили:

=

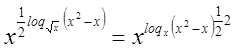В первой части уравнения выполнили преобразования

. Получили уравнение . Все решения содержатся в уравнении.

или .

Ответ: 2.

Пример №16

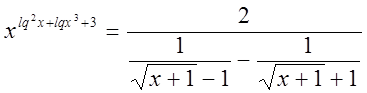
Решение

ОДЗ:

Преобразуем знаменатель дроби в правой части уравнения

; .

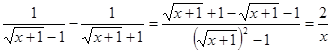, , где

1) , - верно.

2) ,

Пасть , тогда

, или .

Следовательно; или , , .