Дипломная работа: Показательно-степенные уравнения и неравенства

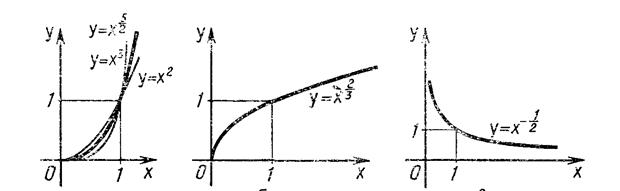
Рис. II.5.

На рисунке II.5. изображен график функции Он заключен между графиками функций у = х² и у = х³ , заданныхна промежутке [0; + оо).

Подобный вид имеет график любой функции вида у = х ^r , где .

На том же рисунке изображен график функции . Подоб­ный вид имеет график любой степенной функции у = х ^r , где .

Степенная функция с отрицательным дробным пока­зателем. Рассмотрим функцию у = х^{- r} , где r — положительная несократимая дробь. Перечислим свойства этой функции.

1) Область определения — промежуток (0; + оо).

2) Функция ни четная, ни нечетная.

3) Функция у = х^{- r} убывает на (0; +оо).

Построим для примера график функции у — х таблицу значений функции:

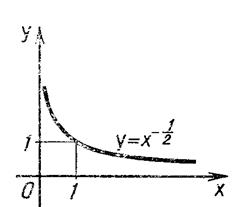Нанесем полученные точки на координатную плоскость и соединим их плавной кривой (см. рис. II.6.).

Подобный вид имеетграфик любой функции

у = х ^r , где r — отрицательная дробь.

Рис. II.6.

II . 2. Показательная функция и ее свойства.

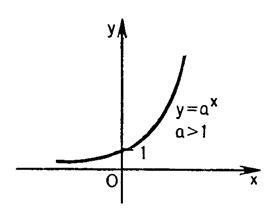Функция, заданная формулой вида у = а^х , где а — некоторое положительное число, не равное единице, называется показатель­ной.

1.Функция у = а^х при а>1 обладает следующими свойст­вами (см. рис. II.7.):

а) область определения — множество всех действительных чисел;

б) множество значений — множество всех положительных чисел;

Рис. II.7.

в) функция возрастает;

г) при х = 0 значение функции равно 1;

д) если x > 0 , то а ^x > 1 ;

е) если х < 0 , то 0 < а^х < 1 .

3. Функция у = а^х при 0<а< 1 обладает следующими свойст­вами (см. рис. II.8.):

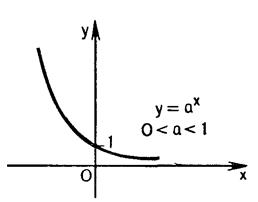а) область определения D ( f )= R ;

б) множество значений E ( f )= R ₊ ;

в) функция убывает;