Дипломная работа: Похідна Фреше та похідна Гато
![]() ,
,
де

Лінійний оператор ![]() називається похідною Фреше відображення
називається похідною Фреше відображення ![]() в точці
в точці ![]() та позначається
та позначається ![]() . Тобто,
. Тобто, ![]() .
.
Відображення, диференційовне в кожній точці множини G називається диференційовним на G.
Доведемо, що похідна диференційованого відображення визначається однозначно. Нехай ![]() – інший неперервний лінійний оператор такий, що
– інший неперервний лінійний оператор такий, що
 ,
,
якщо ![]() . Тоді
. Тоді
 ,
,
якщо ![]() . Покладемо
. Покладемо ![]() , де
, де ![]() – довільний ненульовий елемент простору X. Якщо
– довільний ненульовий елемент простору X. Якщо ![]() , то
, то ![]() і ми знаходимо
і ми знаходимо
 .
.
В силу лінійності ![]() та
та ![]() це означає, що
це означає, що
 ,
,
тобто ![]() . Оскільки оператори
. Оскільки оператори ![]() та
та ![]() в нулі дорівнюють нулю, то
в нулі дорівнюють нулю, то ![]() при будь-яких
при будь-яких ![]() . Однозначність визначення похідної доведено.
. Однозначність визначення похідної доведено.
Приклад 1. Нехай відображення ![]() , де
, де ![]() і
і ![]() відкрито.
відкрито.
Тоді наведені вище означення диференційовності відображення і похідної співпадають з означеннями диференційовності та похідної векторної функції векторного аргументу. В цьому випадку ![]() є лінійним оператором, який визначається матрицею
є лінійним оператором, який визначається матрицею  , де
, де ![]() – координатні функції відображення
– координатні функції відображення ![]() .
.
Приклад 2. Нехай ![]() – гільбертов простір,
– гільбертов простір, ![]() і
і ![]() . Нехай спочатку
. Нехай спочатку ![]() . Тоді
. Тоді
 (1)
(1)
Оскільки ![]() , то
, то
![]() , (2)
, (2)
де ![]() при
при ![]() . Із рівностей (1) та (2) випливає, що
. Із рівностей (1) та (2) випливає, що
![]() ,
,
де ![]() – лінійний по
– лінійний по ![]() функціонал і
функціонал і
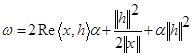 .
.
Оскільки ![]() , то
, то ![]() при
при ![]() . Таким чином,
. Таким чином, ![]() диференційовна в будь-якій ненульовій точці
диференційовна в будь-якій ненульовій точці ![]() простору
простору ![]() і
і
![]() .
.
Нехай тепер ![]() . Тоді
. Тоді ![]() . Покажемо, що не існує елемента
. Покажемо, що не існує елемента ![]() такого, що при всіх достатньо малих
такого, що при всіх достатньо малих ![]()
![]() , (3)
, (3)
де ![]() при
при ![]() . Якщо б це було так, то також
. Якщо б це було так, то також