Дипломная работа: Похідна Фреше та похідна Гато

де при . Але тоді з рівностей (3) та (4) випливає при , що неможливо.

Таким чином, відображення не диференційовне за Фреше в точці .

Приклад 3. Нехай і 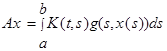, де ядро неперервне в квадраті , – функція двох змінних, визначена в полосі і неперервна в цій області. Тоді – функція, визначена на і яка приймає значення в цьому ж просторі.

Припустимо, що функція не тільки неперервна, але й має частинну похідну, рівномірно неперервну в полосі .

Тоді – диференційовна функція. А саме, для довільної функції маємо

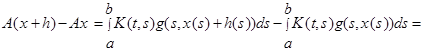
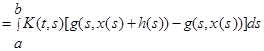
За теоремою Лагранжа,

,

де

. Далі, маємо

.

При , тобто при рівномірно на , також рівномірно на , оскільки функція, неперервна в замкненій обмеженій області , рівномірно неперервна в цій області. Тому

,

де

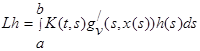і .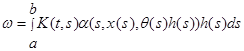

При цьому

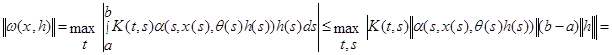
і тому при .

Таким чином, диференційовна за Фреше і

.

Приклад 4. Якщо і границя існує, то диференційовне в точці і . Дійсно, в цьому випадку , де при , і диференційованість очевидна.

Множина відображень, визначених в околі точки , які приймають значення в просторі Y та диференційовних в точці , є лінійною системою , а також оператор диференціювання є лінійним, тобто

,

або, інакше,

.

Далі, з рівності

випливає, що функція , диференційовна в точці , неперервна в цій точці.

Обернене твердження не вірне (приклад 2).