Дипломная работа: Похідна Фреше та похідна Гато
Теорема доведена.
1.3.2 Похідні по підпростору
Поняття, проміжне між похідною Фреше і похідною за напрямком, є похідна по підпростору. Нехай дано відображення ![]() і
і ![]() – підпростір
– підпростір ![]() . Якщо для
. Якщо для ![]() існує неперервний лінійний оператор
існує неперервний лінійний оператор ![]() такий, що для будь-якого
такий, що для будь-якого ![]() , яке задовольняє умові
, яке задовольняє умові ![]() ,
,
![]() ,
,
то відображення f називається диференційовним в точці x по підпростору X0 і позначається ![]() . Якщо X – пряма сума підпросторів X1 та X2 і похідні відображення f по підпросторам X1 та X2 в точці
. Якщо X – пряма сума підпросторів X1 та X2 і похідні відображення f по підпросторам X1 та X2 в точці ![]() існують, то вони називаються частинними похідними відображення f в цій точці і позначаються
існують, то вони називаються частинними похідними відображення f в цій точці і позначаються ![]() і
і ![]() .
.
Лема. Якщо ![]() і відображення
і відображення ![]() має в околі точці
має в околі точці ![]() частинні похідні
частинні похідні ![]() і
і ![]() , неперервні в цій точці, то відображення f диференційовне в точці за Фреше і
, неперервні в цій точці, то відображення f диференційовне в точці за Фреше і
![]() ,
, ![]() .
.
Доведення. Розглянемо
![]()
![]()
![]() ,
,
так як ![]() при
при ![]() і
і ![]()
Лема доведена.
Має місце обернене до леми твердження, причому
![]() .
.
Поняття частинних похідних і попередні результати безпосередньо узагальнюються на випадок, коли X – пряма сума будь-якого скінченого числа підпросторів.
Зауваження. Оскільки в силу відповідності ![]() простори
простори ![]() і
і ![]() є ізоморфними, а з метриками, які породжені нормами
є ізоморфними, а з метриками, які породжені нормами
![]()
є ізометричними, то все вище наведене для частинних похідних переноситься на відображення виду: ![]() де
де ![]() .
.
Нехай тепер ![]() і, як завжди,
і, як завжди, ![]() відкрите, так що
відкрите, так що ![]() де
де ![]() ,
, ![]() . Якщо “координатні функції”
. Якщо “координатні функції” ![]() диференційовні в точці
диференційовні в точці ![]() , то
, то ![]() диференційовне в цій точці і
диференційовне в цій точці і ![]() . Дійсно,
. Дійсно,
![]()
![]() ,
,
Причому
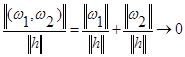 , якщо
, якщо ![]() .
.
Ці результати розповсюджуються на випадок відображень, які приймають значення в декартовому добутку будь-якого скінченого числа просторів.
РОЗДІЛ 2
ПОХІДНІ ФРЕШЕ ТА ГАТО В ПРИКЛАДАХ І ЗАДАЧАХ
1. Довести, що похідна Фреше диференційовного в точці відображення визначається єдиним чином.
Доведення
Нехай ![]() ,
, ![]() – дві похідні Фреше в точці x, тоді
– дві похідні Фреше в точці x, тоді
![]() , де
, де 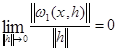 (1)
(1)
![]() , де
, де  (2)
(2)
Розглянемо різницю (2)-(1):