Дипломная работа: Похідна Фреше та похідна Гато
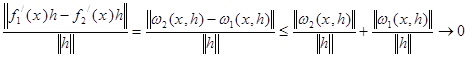, якщо 
Це прямування до нуля нетривіально, тобто
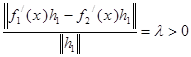
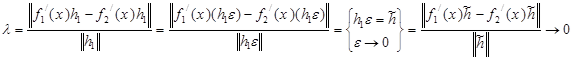
якщо 
.
Тобто, похідна Фреше диференційованого відображення визначається єдиним чином.
2. Довести, що якщо оператор f диференційовний за Фреше в точці x, то f неперервний в цій точці.
Доведення
Якщо та 
, то 
.
3. Довести, що якщо 
, то 
(нульовий оператор).
Доведення.
Нехай оператор 
диференційовний за Фреше, тобто
, де 
Нехай 
, тоді 
(
– нульовий оператор)
, звідки 
(нульовий оператор, який діє на h).
4. Довести, що похідною Фреше лінійного неперервного відображення є саме це відображення.
Доведення.
Нехай оператор диференційований за Фреше, тобто
, де
