Дипломная работа: Похідна Фреше та похідна Гато

,

звідки й випливає наведене твердження.

Слід зазначити, що відображення та , які мають область визначення в одному і тому просторі, діють в різні простори, а саме , а . Якщо диференційовне всюди на G, то , .

1.2 Основні теореми

Теорема 1 (про диференційовність композиції відображень). Нехай – лінійні нормовані простори й задані відображення , де , – відкрита множина; , де , – відкрита множина. Якщо множина не порожня , відображення диференційовне в точці , а диференційовне в точці , то складне відображення диференційовне в точці і

.

Доведення. Насамперед, якщо достатньо мале, то в силу відкритості множин та й неперервності відображень і відповідно в точках та , точки і не вийдуть за границі множин та . Далі маємо

.

Оскільки диференційовне в точці , то

,

де , якщо . В свою чергу,

де , якщо . Тому

Вираз є лінійним оператором по , і залишається довести, що , якщо .

Маємо

.

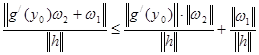Перший доданок справа прямує до нуля, оскільки , якщо . Прямування до нуля другого доданка можна довести так. Оскільки диференційовне в точці , то , якщо . Тому для будь-якого знайдеться , таке, що , якщо . В свою чергу, в силу неперервності в точці для даного знайдеться таке, що , якщо . Далі, оскільки диференційовне в точці , то знайдеться таке, що 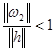, якщо . Нехай . При маємо

,

і оскільки довільне, то це означає, що , якщо .

Теорему доведено.

Приклад 5. Розглянемо відображення , диференційоване на відкритій множині , і точки такі, що . Тоді функція , визначена рівністю

,

диференційовна на і .

Приклад 6. Нехай відображення диференційоване на і – лінійний неперервний оператор. Тоді – відображення, диференційовне на , і .

Наступна теорема є аналогом теореми Лагранжа про скінченні прирости дійсних функцій дійсних аргументів.

Теорема 2 (про скінченні прирости). Нехай відображення диференційовне на і відрізок цілком входить до . Тоді

.

Доведення. Розглянемо відображення , де . Це відображення неперервне на як композиція неперервних відображень та , і в силу теореми 1 диференційовне всередині , при цьому