2) f ( t ) возрастает не быстрее некоторой показательной функции , при t 0 , где M 0, s₀ 0 — некоторые действительные постоянные, s ₀ называют показателем роста функции f(t) .

3) На любом конечном отрезке a , b положительной полуоси Ot функция f (t ) удовлетворяет условиям Дирихле, т.е.

a) ограничена,

b) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода,

c) имеет конечное число экстремумов.

Функции, удовлетворяющие этим трем требованиям, называются в операционном исчислении изображаемыми по Лапласу или оригиналами .

Простейшим оригиналом является единичная функция Хевисайда

Если функция удовлетворяет условию 2 и не удовлетворяет 1, то произведение будет удовлетворять и условию 1, т.е. будет оригиналом. Для упрощения записи будем, как правило, множитель H (t ) опускать, считая, что все рассматриваемые функции равны нулю при отрицательных значениях t .

Интегралом Лапласа для оригинала f (t ) называется несобственный интеграл вида

,

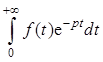где – комплексный параметр.

Теорема.

Интеграл Лапласа абсолютно сходится в полуплоскости (то есть изображение F (p ) заведомо определено при ), где s ₀ – показатель роста f (t ).

∆ При получаем:

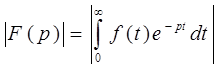, но по свойству модулей .

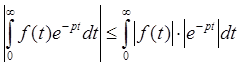Заметим, что по определению оригинала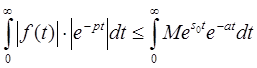

.

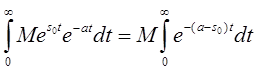Вычислим этот интеграл:

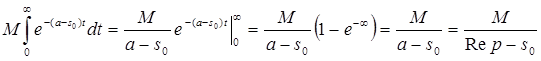
То есть получаем что F (p ) существует при

▲

Замечание . Из доказательства теоремы следует оценка:

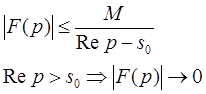
при

Определение 2 . Изображением по Лапласу функции f (t ) называется функция комплексного переменного p = s + i σ, определяемая соотношением

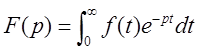(1)

Тот факт, что функция F (t ) является изображением оригинала f (t ), символически это записывается так:

или (2)

§2. Основные теоремы операционного исчисления

2.1 Свертка оригиналов.