Дипломная работа: Применение операционного исчисления при решении дифференциальных уравнений

где a_k –действительные числа.

Требуется найти решение данного дифференциального уравнения, удовлетворяющее начальным условиям

x (0)= x ₀ , x `(0)= x `₀ , …, x ^{( n -1)} (0)= x ₀ ^{( n -1)}

где x ₀ , x `₀ , …, x ₀ ^{( n -1)} – заданные числа.

Будем предполагать, что искомая функция x (t ), все ее производные, а также функция f (t ) являются оригиналами.

Пусть . По формулам дифференцирования оригиналов

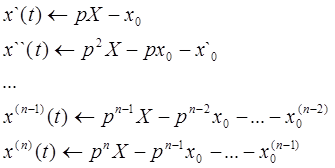
Перейдем от данного дифференциального уравнения к уравнению в изображениях

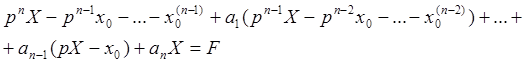
Перепишем его так , где , а

Находим так называемое операторное решение уравнения

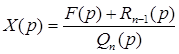
Найдя оригинал x (t ) по его изображению X (p ) , мы получим тем самым решение задачи Коши для исходного дифференциального уравнения.

7. Примеры

Пример 1.

Найти решение дифференциального уравнения x (t )4x (t )5x (t )0,

удовлетворяющее условиям x (0) 0, x (0) 1.

Решение . Запишем уравнение в изображениях

Вынесем Х за скобки

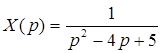
Найдем оригинал используя выведенные ранее значения в таблице приложения:

искомое решение -

Пример 2.