Дипломная работа: Применение операционного исчисления при решении дифференциальных уравнений

Таким образом, при t =0 получаем u=0, при получаем и

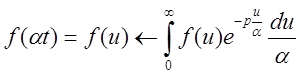
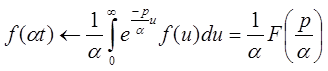
2.3 Теорема запаздывания.

для t > τ > 0

Таким образом, запаздывание аргумента оригинала на положительную величину приводит к умножению изображения оригинала без запаздывания F(p) на e^pt .

2 .4 Теорема смещения.

Для a >0 имеет место соотношение:

∆

Из определения изображения имеем:

2.5 Теорема упреждения.

При а > 0 имеет место соотношение:

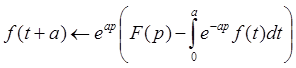
2.6 Умножение оригиналов

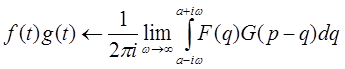
2 .7 Дифференцирование оригинала

Если и – оригиналы и , то

(2.7.1)

В самом деле, исходя из формулы Ньютона – Лейбница, в силу (2.1.1) будем иметь

.

Тогда по теореме 1

.

Отсюда , что и требовалось доказать.

Применив формулу (2.7.1) дважды, получим

и т.д. В частности, если , то , т.е. в этом случае дифференцирование оригинала сводится к умножению его изображения на p .

2.8 Дифференцирование изображения

Если , то , то есть умножению оригинала на (- t ) соответствует производная от изображения F (p ).

Обобщение:

Путем последовательного дифференцирования по параметру p равенства получим:

2 .9 Интегрирование оригинала