Дипломная работа: Применение операционного исчисления при решении дифференциальных уравнений

.

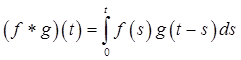Функции f (t ) и g (t ) называются компонентами свертки .

Найдем для примера свертку произвольного оригинала и единичной функции Имеем .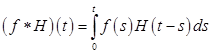

Так как при то

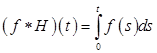. (2.1.1)

Теорема 1. Если и, то

.

∆

Действительно, по определению интеграла Лапласа имеем

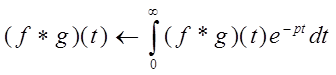
Воспользуемся определением свертки:

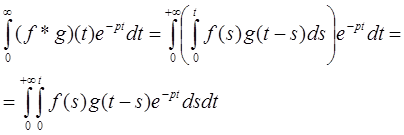
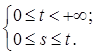
Изменив порядок интегрирования в двойном интеграле, получим

.

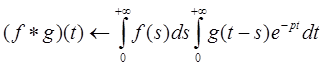Введем вместо t новую переменную . Тогда

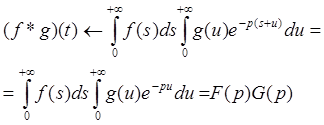
что и требовалось доказать. ▲

Свойство линейности.

Для любых комплексных постоянных и :

∆

Это свойство вытекает из свойства линейности интеграла.

Домножим равенство 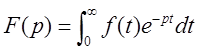на α: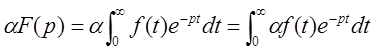

Так как , то , то есть

2 .2 Теорема подобия.

Для любого постоянного a > 0:

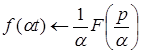
Умножение аргумента оригинала на положительное число  приводит к делению изображения и его аргумента на это число .