Отсюда

Согласно приложению

,

Собирая оригиналы всех слагаемых, представляющих Y (p ), получаем искомое решение:

если .

Пример 6

Операционный метод может быть применён для решения нестационарных задач математической физики. Рассмотрим случай, когда некая функция u(x,t) зависит лишь от пространственной координаты x и времени t.

Для уравнения теплопроводности будем решать краевую задачу:

a ² =const , u (x ,0)=φ(x ) - начальные условия и u (0,t )=ψ₁ (t ), u (l , t )=ψ₂ (t ), 0 ≤ x ≤ l – краевые условия.

Пусть все функции являются оригинальными. Обозначим

- изображение по Лапласу.

Тогда

Тогда краевые условия:

Уравнение в изображениях:

Библиографический список.

1. Старков В.Н. Операционное исчисление и его применения. Учебн. пособ.-СПб, 2000.

2. Белослюдова В.В., Дронсейка И.П.Специальные разделы математики.Часть 1. Элементы теории функций комплексной переменной. Операционное исчисление: Курс лекций для студентов второго курса специальностей 050702, 050716 / ВКГТУ. – Усть – Каменогорск, 2006.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. М., 2005

4. Ершова В.В. Импульсные функции. Функции комплексной переменной. Операционное исчисление. Под ред. В.И. Азаматовой. Минск, 1976

Приложение

Таблица оригиналов и их изображений.

Оригинал	Изображение	Оригинал	Изображение
1
t
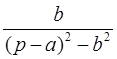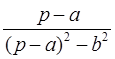
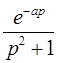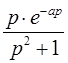