.

Так как , то

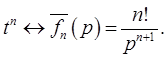
Полученные с помощью формулы (1) изображения некоторых функций сведены в таблицу (см. приложение). Ее можно использовать для нахождения изображений функций.

§4. Отыскание оригинала по изображению

Для нахождения оригинала f(t) по известному изображению F(p) нужно использовать формулы обращения Римана-Меллина

.

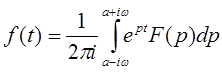Если функция f(t) является оригиналом, т.е. удовлетворяет условиям 1-3 определения 1 и F(p) служит ее изображением, то в любой точке своей непрерывности функция f(t) равна:

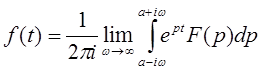
Формула обращения Римана-Меллина дает выражение оригинала f(t) через изображение F(p) , причем α – произвольное число, удовлетворяющее неравенству α>s₀ .

Вычисление оригинала по формуле Римана-Меллина довольно трудоёмко, поэтому на практике при решении задач применяют другие методы, которые рассматриваются ниже.

4.1 Разложение на простейшие дроби.

Если 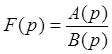есть дробно-рациональная функция, причем степень числителя A (p ) меньше степени знаменателя B (p ), то эту дробь разлагают на сумму простых дробей и находят оригиналы для каждой простой дроби либо непосредственно по формуле (1), либо по таблице (см. приложение).

Пример 1. Найти оригинал по изображению.

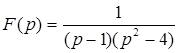
Разложим функцию на сумму дробей:

Найдем методом неопределенных коэффициэнтов А, В, С :

Тогда

Воспользуемся приложением:

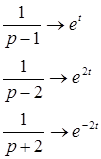
В итоге оригинал равен

4.2. Первая теорема разложения

Теорема . Если изображение искомой функции может быть разложено в степенной ряд по степеням , т.е.

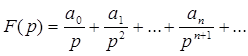
(причем этот ряд сходится к F ( p ) при 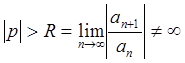), то оригинал имеет вид

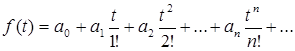
(причем ряд сходится при всех значениях t ).

§5 Решение задачи Коши для обыкновенных линейных

дифференциальных уравнений с постоянными коэффициентами

Рассмотрим линейное дифференциальное уравнение