Дипломная работа: Разностные схемы для уравнения переноса на неравномерных сетках

1.4 Разностная схема

Как правило, дифференциальное уравнение решается с некоторыми дополнительными условиями - начальными (задача Коши), краевыми (краевая задача) либо и с начальными, и с краевыми условиями (смешанные задачи). Эти дополнительные условия при переходе к разностным уравнениям надо так же аппроксимировать.

Пусть имеем некоторую дифференциальную задачу, записанную в виде

Lu=f(x), xG (8)

с дополнительным условием

lu=ц(x), xГ. (9)

Введем в области Г сетку

и поставим в соответствие задаче (8), (9) разностную задачу

L_h y_h =f_h , xw_h , (10)

L_h y_h =ц_h , xг_h . (11)

Функция y_h (x), f_h (x), ц_h (x) зависят от шага сетки. Меняя h, получаем множества функций {y_h }, {f_h }, {ц_h }, зависящих от параметра h. Таким образом, мы рассматриваем не одну разностную задачу, а семейство задач, зависящее от параметра h. Это семейство задач называется разностной схемой.

Рассмотрим примеры разностных схем, аппроксимирующих дифференциальные задачи.

Пример 1. Имеем задачу Коши

, 0<x≤1, л = const

.

Используем аппроксимации:

;

.

После этого имеем разностную схему:

Расчетный алгоритм имеем вид

Пример 2. Рассмотрим задачу Коши.

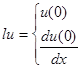
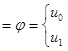
Воспользуемся следующими аппроксимациями: