Дипломная работа: Разностные схемы для уравнения переноса на неравномерных сетках

После этого имеем разностную схему

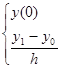
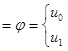
1.5 Корректность разностной схемы

Пусть имеем дифференциальную задачу

, (12)

(13) и на сетке аппроксимируем ее разностной схемой

(14)

(15)

Задача (12), (13) поставлена корректно, если выполнены условия:

1) задача однозначно разрешима при любых правых частях

2) решение задачи непрерывно зависит от правых частей т.е.

_H ≤ M₁ ∙_H +M₂ ∙_{H .}

Аналогично определяется понятие корректности разностной схемы (14), (15). Говорят, что разностная схема (14), (15) корректна, если при всех достаточно малых │h│< h₀ :

1) решение y_h разностной схемы существует и единственно для всех входных данных f _h H_h , ц_h H_h ;

2) существуют постоянные M₁ >0, M₂ >0 не зависящие от h и такие, что при любых f _h H_h , ц_h H_h справедлива оценка

_Hh ≤ M₁ ∙_Hh +M₂ ∙_{Hh .} (16)

Свойство 2), означающее непрерывную зависимость, равномерную относительно h, решения разностной схемы от правых частей, называется устойчивостью разностной схемы. Рассмотрим примеры.

Пример 1. Пусть имеем задачу:

(17)

Точным решением задачи (17) является функция

Если ввести новую функцию то получим задачу

(18)

Решением задачи (18) является функция

Задачу (18) аппроксимируем на равномерной сетке = {x_i =ih, i=0,n} схемой:

(19)