Дипломная работа: Решение задач на экстремум

Отсюда видно, что наибольшая площадь получится в том случае, когда мы сделаем глубину канала х = Р/4. Тогда окажется ширина у равной Р/2, а наибольшая площадь равной Р2/8.

Пример 3:

Найти наименьшее и наибольшее значение функции y=4x+6|x-2|-x2 на отрезке [-1;3].

Решение:

y=-( x2-4x+4-4)+ 6|x-2|=-(x-2)2 +6|x-2|+4. Так как а2=|а|2, то

y= -|x-2|2+6|x-2|+4. Пусть t=|x-2|. Поскольку -1 ≤ х ≤ 3, то 0 ≤ t ≤ 3. При этом y=-t2+6t+4 возрастает и, следовательно,

miny(t)=y(0)=4, maxy(t)=y(3)=13.

[0;3] [0;3]

Если t=0, то x=2. Если t=3, то |x-2|=3

Но по условию х[-1;3], поэтому остается только значение х=-1.

Ответ: miny(х)=y(2)=4, maxy(х)=y(-1)=13.

[-1;3] [-1;3]

Оценок и неравенств

Теорема 2.

Функция х + , где а > 0 и x > 0, имеет наименьшее значение равное 2. Это наименьшее значение получается при х = .

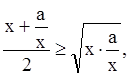или

Очевидно, что .

Отсюда следует, что наименьшее значение получается при х – 2 = , т.е. при х = 6, а само наименьшее значение равно 10.

Теорема 3.

Если сумма двух положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда оба сомножителя принимают одинаковые значения.

Доказательство.

Пусть х и у - положительные переменные величины и пусть х + у = с, где с - постоянная величина. Применяя неравенство о среднем арифметическом и среднем геометрическом, получим:

или, наконец,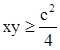

Отсюда очевидно, что наибольшее значение произведения ху равно с2/4 и получается оно при х = у.

Теорема 4.

Если сумма n положительных переменных величин постоянна, то произведение этих переменных имеет наибольшее значение, когда все эти переменные принимают одинаковые значения. (Эта теорема является обобщением теоремы 3.)

Доказательство.

Пусть х1, х2, …, хn - положительные переменные величины и пусть х1 + х2 + … + хn = с, где с - постоянна. По теореме Коши о среднем арифметическом и среднем геометрическом имеем: