Дипломная работа: Решение задач на экстремум

Пример 1:

Найти наибольшее значение функции х4(32-х4).

Поиски решения.

Данная функция принимает отрицательные значения при , а при -положительные. Поскольку ее наибольшее значение надо искать среди значений х меньших , чем

Если мы положим х4 = у, то задача сведется к нахождению наибольшего значения многочлена второй степени, имеющего вид:

- у2 +32у.

Однако если проявить наблюдательность и заметить, что сумма множителей х4 и (32 - х4) является величиной постоянной, то можно воспользоваться теоремой 3 и решить задачу проще.

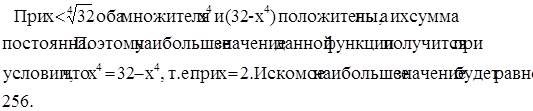
Пример 2:

Найти наибольшее значение функции 3х2 - 2х3 при 0<х<3/2.

Поиски решения.

Во-первых, выясним, почему здесь на независимую переменную х наложены ограничения. Если допустить, что х<0, то данная функция не будет иметь наибольшего значения, так как она будет неограниченно возрастать при неограниченном возрастании абсолютной величины аргумента х, принимающего отрицательные значения. Например, при х = -1000 значение данной функции будет равно 3 10002 + 2 10003. Если же допустить, что х>3/2, то окажется, что 3х2 - 2х3<0. При значениях же х, заключенных между нулем и числом 3/2, все значения данной функции будут положительными. Поэтому наибольшее значение надо искать при таких значениях х, которые удовлетворяют неравенствам 0<х<3/2.

Если мы запишем нашу функцию в виде х2 (3 - 2х), то увидим, к сожалению, что сумма сомножителей х2 и (3 - 2х) не постоянна. И вот тут-то надо проявить изобретательность и записать данную функцию в виде произведения трех сомножителей, а именно так: х х (3 - 2х).

Решение. Очевидно, что 3х2 - 2х3 = х2(3 - 2х) = х х (3 - 2х).

При условиях нашей задачи в последнем произведении все три множителя положительны и их сумма равна 3, т.е. является величиной постоянной.

По теореме 4 наша функция будет иметь наибольшее значение при условии, что х = х = 3 - 2х, т.е. при х = 1. И само наибольшее значение нашей функции будет равно тоже 1. Если мы положим, например, х = 5/4, то значение нашей функции окажется равным 25/32, т.е. окажется меньшим единицы.

Пример 3:

Найти наибольшее значение функции

y=4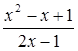 на интервале (-∞;).

Решение:

y=4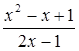==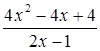=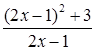2x-1+.

Так как по условию х<1/2, то 2х-1<0 и <0. Воспользуемся неравенством | at+b/t | ≥2

для случая t<0. Тогда y=2х-1+≤-2, причем знак неравенства достигается тогда и только тогда, когда

2х-1=, и 2х-1<0 .

И последней системы находим х=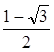

Ответ: maxy(x)=y()=-2

(-∞;)

2.2 Универсальный метод решения задач на экстремумы

Мы рассмотрели довольно много задач на нахождение экстремумов. Те приемы, которыми мы решали эти задачи, оказались весьма разнообразными и порой, довольно искусственными. Дело обстоит так, что почти для каждой задачи на экстремум приходилось «изобретать» подходящий для нее прием. Возникает поэтому вопрос: а нет ли достаточно общего приема решения задач на экстремумы? Такой прием есть. Его дает математический анализ.