Дипломная работа: Решение задач на экстремум
Если функция у = f(х) (имеющая локальную производную) при х = х0 принимает локальный максимум или минимум, то производная от этой функции при х = х0 обращается в 0.
Геометрически это означает, что касательная к графику функции в соответствующей точке его параллельна оси х-ов
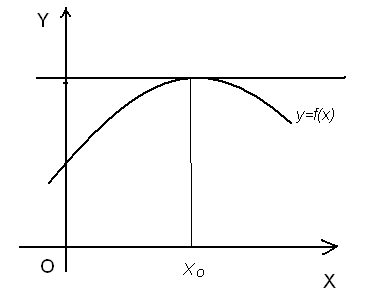
Теорема Ферма очень наглядна. И все же докажем ее.
Пусть х0 - точка максимума функции у = f(x), т.е. при х = х0 эта функция принимает наибольшее значение. Дадим х0 достаточно малое приращение h. Новое значение аргумента х0 + h будет достаточно близким к х0, и т.к. при х = х0 данная функция имеет максимум, то f(x0+h)-f(x0)≤0. Поэтому
![]()
Если же дать х0 отрицательное приращение (достаточно малое по абсолютной величине), то получим:
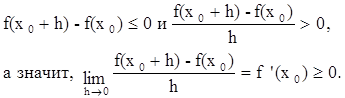
Оказалось, что одно и то же число f '(x0) не положительно и неотрицательно. Это означает, что это число равно 0, т.е. f '(x0) = 0. Рассуждения в случае минимума аналогичны.
Чему же учит нас теорема Ферма? Она учит нас тому, что значения аргумента, при которых данная функция f(x) имеет локальные минимумы, следует искать среди корней уравнения f '(x) = 0. Она выражает необходимое условие экстремума:
Для того чтобы функция (имеющая производную) имела при х = х0 максимум или минимум, необходимо, чтобы производная при этом значении х была равна 0.
Необходимо, но не достаточно! Производная может быть равна 0, и все же при этом значении х функция экстремума может и не иметь. Так, например, производная функции у = х3 (у' = 3х2) при х = 0 обращается в 0, но эта функция при х = 0 экстремума не имеет (рис.2). Значит, уравнение f '(х) = 0 дает лишь «подозрительные» на экстремум значения х.
Как же из этих «подозрительных» значений выделить те, при которых рассматриваемая функция действительно имеет экстремумы?
Как для выделенных значений установить вид экстремума?
По этим вопросам мы ограничимся соображениями, источником которых является наглядность. Рассмотрим рисунок, на котором изображены максимум и минимум функции у = f(x). По этому рисунку установим, какие по знаку значения принимает производная функция f '(x) для значений х, достаточно близких к х0, меньших и больших его. Если при х = х0 данная функция имеет максимум, то для значений х, меньших х0, но достаточно близких к х0, производная будет положительна, а для больших- отрицательна, т.к. в первом случае касательная к графику функции образует с положительным направлением оси х-ов острый угол, а во втором- тупой.
Если же при х = х0 функция принимает минимальное значение, то получается наоборот. Таким образом, будет ли «подозрительная» точка х0 точкой экстремума и, если будет, то какого именно (максимума или минимума), зависит от значений, принимаемых в достаточной близости слева и справа от точки х0 производной функцией. Все возможные случаи можно записать в следующей таблице.
| х0+Δх, Δх<0 | х0 | х0+Δх | Поведение f(x) |
|
f '(x) f '(x) f '(x) f '(x) |
+ - + - |
0 0 0 0 |
- К-во Просмотров: 947
Бесплатно скачать Дипломная работа: Решение задач на экстремум
|