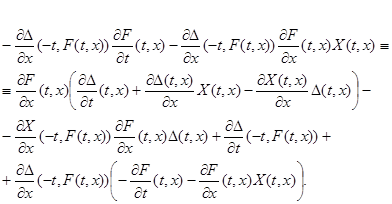Дипломная работа: Системы эквивалентные системам с известными качественными свойствами решений

Лемма 3.1. Для любых трёх вектор-функций

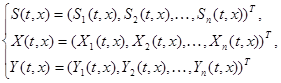
имеет место тождество

Доказательство.

Будем преобразовывать левую часть тождества

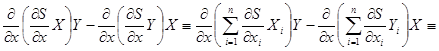
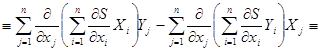
Лемма доказана.

Лемма 3.2. Пусть есть отражающая функция системы с непрерывно дифференцируемой правой частью. Тогда для каждой непрерывно дифференцируемой вектор-функции функция

удовлетворяет тождеству

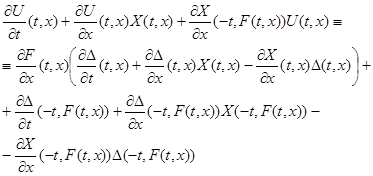
Доказательство.

Подставив функцию в выражение , придем к следующим тождествам:

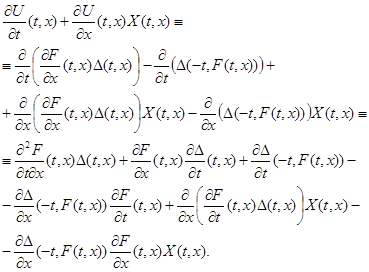
Выразим из соотношения частную производную , подставим в последнее тождество и будем преобразовывать получившееся выражение:

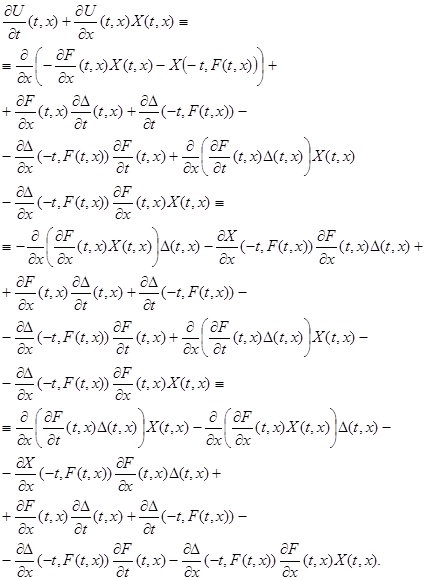
Применив к первым двум слагаемым последней части этой цепочки тождеств тождество придем к следующим соотношениям: