Дипломная работа: Системы эквивалентные системам с известными качественными свойствами решений

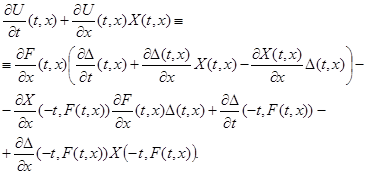
Учитывая определение функции , полученное тождество можно переписать в виде

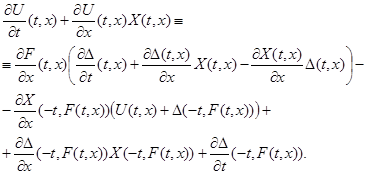
Мы пришли к соотношению

Прибавив к левой и правой частям этого соотношения выражение , придем к нужному нам тождеству и тем самым докажем лемму.

Лемма доказана.

Теорема 3.1. Пусть вектор-функция является решением дифференциального уравнения в частных производных

Тогда возмущенная дифференциальная система где произвольная непрерывная скалярная нечетная функция, эквивалентна дифференциальной системе в смысле совпадения отражающих функций.

Доказательство. Пусть отражающая функция системы Следовательно, эта функция удовлетворяет дифференциальному уравнению . Покажем, что помимо этого уравнения при условиях теоремы она удовлетворяет тождеству

С этой целью введем функцию по формуле . Согласно предыдущей лемме, эта функция удовлетворяет тождеству . При условиях доказываемой теоремы, с учетом соотношения это тождество переписывается в виде

Кроме того, поскольку для всякой отражающей функции верно тождество , имеют место соотношения

Поставим следующую задачу Коши для функции :

Решение этой задачи существует и единственно [6, с.66]. Таким образом, имеет место тождество влекущее за собой тождество .

Теперь покажем, что отражающая функция дифференциальной системы является также и отражающей функцией дифференциальной системы . Для этого нужно проверить выполнение основного соотношения , которое в данном случае должно быть переписано в виде

Последовательно преобразовывая левую часть последнего соотношения и учитывая нечетность функции , приходим к следующей цепочке тождеств:

Оба слагаемых, стоящих в квадратных скобках, тождественно равны нулю. Первое - потому, что для отражающей функции системы верно тождество , второе - потому, что при условиях теоремы верно тождество . Следовательно, тождество выполняется и функция является отражающей функцией системы .

Теорема доказана.

Следствие3.1. Пусть функции являются решениями дифференциального уравнения в частных производных . Тогда все дифференциальные системы вида