Дипломная работа: Собственные колебания пластин
Если корни характеристического уравнения чисто мнимые, т.е. ![]() . Общим решением уравнения (1.3.1) будет
. Общим решением уравнения (1.3.1) будет
|
Если предположить, что характеристическое уравнение имеет равные корни ![]() , то одно частное решение будет иметь вид
, то одно частное решение будет иметь вид
![]() .
.
Второе частное решение будет
![]() .
.
Тогда общее решение уравнения (1.3.1) можно представить в виде
|
Глава II Нахождение функции, описывающей собственные колебания мембраны
2.1 Основные определения
В этой главе использованы следующие обозначения
· ![]() - частная производная функции
- частная производная функции ![]() по
по ![]() ;
;
· ![]() - производная функция одной переменной.
- производная функция одной переменной.
Мембраной называется плоская пластинка, не сопротивляющаяся изгибу и сдвигу. Мы будем рассматривать поперечные колебания мембраны, в которых смещение перпендикулярно к плоскости мембраны. Отклонение точек мембраны от плоскости xOy будем обозначать через функцию ![]() , которая зависит от координат точки ( x , y ) и от времени t . Вывод дифференциальных уравнений задач математической физики сопровождается целым рядом допущений как механических, так и геометрических. Так при выводе уравнения колебания прямоугольной мембраны мы пренебрегли квадратом частных производных
, которая зависит от координат точки ( x , y ) и от времени t . Вывод дифференциальных уравнений задач математической физики сопровождается целым рядом допущений как механических, так и геометрических. Так при выводе уравнения колебания прямоугольной мембраны мы пренебрегли квадратом частных производных
|
 .
.
В результате получается следующее уравнение колебаний прямоугольной мембраны
![]() .
.
В случае рассмотрения мембраны круглой формы полезно перейти к полярным координатам. Пусть мембрана в состоянии покоя занимает круг радиуса ![]() с центром в начале координат. Введем полярные координаты
с центром в начале координат. Введем полярные координаты ![]() ,
, ![]() . Уравнение границы круга будет при этом
. Уравнение границы круга будет при этом ![]() . Отклонение точек мембраны является теперь функцией полярных координат
. Отклонение точек мембраны является теперь функцией полярных координат ![]() и
и ![]() и времени t :
и времени t :
![]() .
.
Выражение для оператора 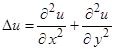 в полярных координатах имеет вид
в полярных координатах имеет вид
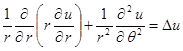 ,
,
Тогда уравнение колебаний мембраны (2.1.1) перепишется в виде
|
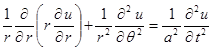 .
.
В данной главе нам еще понадобится определение ортогональных функций в следующем виде:
Система функций ![]() называется ортогональной на интервале
называется ортогональной на интервале ![]() , если интеграл от произведения любых двух различных функций системы равен нолю:
, если интеграл от произведения любых двух различных функций системы равен нолю: 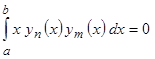 (
(![]() ). Это условие ортогональности отличается от обычного тем, что под интегралом содержится множитель
). Это условие ортогональности отличается от обычного тем, что под интегралом содержится множитель ![]() , в таких случаях говорят об ортогональности с весом
, в таких случаях говорят об ортогональности с весом ![]() [1].
[1].
2.2 Собственные колебания прямоугольной мембраны
Процесс колебания плоской однородной мембраны описывается уравнением
|
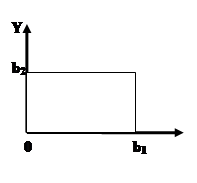
|
Пусть в плоскости ( x , y ) расположена прямоугольная мембрана со сторонами b1 и b2 , закрепленная по краям. Ее колебание вызывается с помощью начального отклонения и начальной скорости.
Для нахождения функции ![]() , характеризующей отклонение мембраны от положения равновесия (прогиб), нужно решить уравнение колебаний при заданных начальных условиях
, характеризующей отклонение мембраны от положения равновесия (прогиб), нужно решить уравнение колебаний при заданных начальных условиях
|
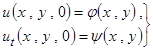
и граничных условиях
|
![]() .
.
Краткое решение задачи (2.2.1) – (2.2.3) приведено в книге [8], где были получены следующие результаты.
Функция ![]() имеет вид
имеет вид
![]() ,
,
где ![]() - собственные функции, соответствующие собственным значениям
- собственные функции, соответствующие собственным значениям ![]() (полученным в результате применения метода Фурье) и определяющиеся формулой
(полученным в результате применения метода Фурье) и определяющиеся формулой
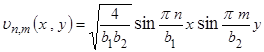 .
.