Дипломная работа: Собственные колебания пластин

1) При задача не имеет нетривиальных решений. Общее решение уравнения имеет вид

,

т. к. характеристическое уравнение имеет корни .

Учитывая граничные условия, получаем:

т.к. - действительно и положительно, то .

2) При нетривиальных решений тоже не существует.

3) При общее решение уравнения имеет вид

.

Учитывая граничные условия, получаем:

, т.к. мы ищем нетривиальные решения, , следовательно

Итак, только при значениях равных , существуют нетривиальные решения задачи (2.2.11) и имеют вид

.

Они определяются с точностью до произвольного сомножителя, который мы положили равным единице.

Аналогично получаем решение задачи (2.2.12):

Собственным значениям , таким образом, соответствуют собственные функции

,

где - некоторый постоянный множитель. Выберем его так, чтобы норма функций с весом единица была равна единице

.

Вычислим отдельно интегралы в равенстве:

(2.2.13)

?????,

.

Число собственных функций, принадлежащих зависит от количества целочисленных решений n и m уравнения

.

Собственным значениям соответствуют решения уравнения :

,

где и - произвольные константы.

Возвращаясь к начальной задаче для уравнения с дополнительными условиями (2.2.4) – (2.2.5), получаем, что частные решения будут иметь вид

.

Тогда общее решение запишется в виде

,

где определяется формулой (2.2.13), а коэффициенты и равны:

,

.

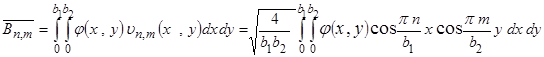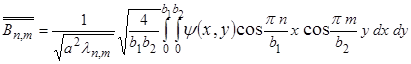В задачах, рассмотренных в этом параграфе, необходимо было найти функцию, описывающую отклонение мембраны от положения равновесия при одинаковых начальных условиях, но при различных граничных условиях. В результате были получены две разные функции. Таким образом, можно сказать, что прогиб мембраны напрямую зависит от граничных условий.