Дипломная работа: Собственные колебания пластин
,
.
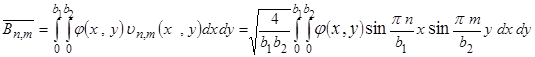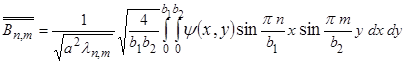Найдем решение задачи при других граничных условиях.
Итак, для нахождения функции 
, характеризующей прогиб мембраны мы должны решить уравнение колебаний мембраны (2.2.1) при заданных начальных условиях
|
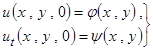
и граничных условиях
|
.
|
|
? ????????? (2.2.1) ?, ??????? ??? ????? ????????? ?? 
(??? ???? ?? ?? ?????? ???????, ?. ?. 
), ???????? 
.
Чтобы функция (2.2.6) была решением уравнения (2.2.1), равенство (2.2.7) должно удовлетворяться тождественно, т.е. для любых значений переменных 
, 
, 
. Правая часть равенства (2.2.7) является функцией только переменных ( x , y ) , а левая – только t . Фиксируя, например, некоторые значения x и y и меняя t (или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно 
.
|
,
где 
- постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
|
: 
,
а для функции 
следующую краевую задачу:
|
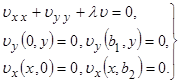
Таким образом, сама задача о собственных значениях состоит в решении однородного уравнения в частных производных при заданных граничных условиях. Снова применим метод разделения переменных. Пусть
|
? ????????? 
?, ??????? ??? ????? ????????? ?? 
, ???????? ??? ? ???? 
.
Правая часть равенства (2.2.10) является функцией только переменной y , а левая – только x . Фиксируя, например, некоторые значения x и меняя 
(или наоборот), получаем, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение, пусть оно равно 
.
Тогда из данного соотношения получаем два однородных дифференциальных уравнения второго порядка:
1. 
2. 
где 
и - постоянные разделения переменных, причем 
. При этом граничные условия для 
и 
вытекают из соответствующих условий для функции 
.
,
,
,
.
Получаем следующие одномерные задачи на собственные значения:
(2.2.11) 
(2.2.12) 