Дипломная работа: Статистичний аналіз тенденцій захворюваності в Україні

РОЗДІЛ 1. ЛІНІЙНА РЕГРЕСІЯ

1.1 Метод найменших квадратів. Властивості оцінок найменших квадратів. Оцінювання σ² . Теорія розподілів. Оцінювання при наявності лінійних обмежень

Нехай Y - випадкова величина, яка флуктуює навколо деякого невідомого параметра η, тобто Y = η + ε, де ε - флюктуація або „помилка". Наприклад, ε може бути „природною" флуктуацією, яка властива самому експерименту, або може бути помилкою у вимірюванні значення η.

Припустимо, що η можна подати у вигляді

η = β₀ + β₁ x₁ + … + β_{p -1} x_{p -1} ,

де х₁ , х₂ , ..., x_{p -1} - відомі постійні величини, а β_j (j = 0, 1, .., p - 1) - невідомі параметри, які підлягають оцінюванню. Якщо значення х_j , j = 0, 1, .., p – 1 змінюються і при цьому спостерігається n значень Y₁ , Y₂ , ...,Y_n змінною Y, то

Y_i = β₀ + β₁ x_{i 1} + … + β_{p -1} x _{i , p -1} + ε_i , i = 1, 2, ..., n, (1.1.1)

де x_ij i-те значенням для х_j . В матричному вигляді (1.1.1) запишеться

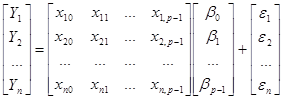
або

Y = Xβ + ε, (1.1.2)

де x₁₀ = x₂₀ = ... = x_{n 0} = 1.

Означення. Матриця X = Х^{( n p )} називається регресійною матрицею. При цьому значення x_ij зазвичай вибираються так, щоб стовпці цієї матриці були лінійно незалежними, тобто ранг матриці X дорівнював р. Проте в деяких випадках при плануванні експерименту елементи матриці X обираються рівними тільки нулю і одиниці, і її стовпці можуть виявитися лінійно залежними. В цьому випадку матрицю X називають матрицею плану.

Далі х_j називатимемо регресором, а Y – відкликом.

Модель (1.1.1) або (1.1.2) лінійна по відношенню до невідомих параметрів β_j , тому її називають лінійною моделлю.

Одним з методів знаходження оцінки вектора β є метод найменших квадратів. Цей метод полягає в мінімізації суми по відношенню до вектора β. Точніше, вважаючи θ = Xβ, мінімізуємо величину ε'ε = ||Y- θ||² по відношенню до θ [Х] = Ω, де Ω - образ оператора X, тобто Ω = {у: у = Хх} для деякого х. Якщо змінювати значення вектора θ в межах Ω, то ||Y- θ||² (квадрат довжини вектора Y- θ) досягає мінімуму при тому значенні θ = , для якого (Y - ) Ω (рис.1.1.1). Тому

X'(Y - ) = 0,

Або

Х' = Х'Y. (1.1.3)

Вектор визначається однозначно, оскільки він є ортогональною проекцією вектора Y на Ω. Якщо тепер стовпці матриці X лінійно незалежні, то існує

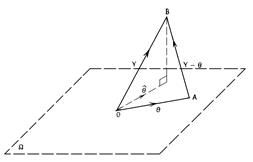
Рис. 1.1.1 Метод найменших квадратів полягає у знаходженні такої точки А, для якої відстань АВ мінімальна

єдиний вектор , для якого = X. Підставлячи в (1.1.3), одержуємо нормальне рівняння

Х'Х = Х'Y. (1.1.4)

Оскільки ми припускаємо, що матриця X має ранг р, то матриця Х'Х додатньо визначена і, отже, не вироджена. Тому рівняння (1.1.4) має єдиний розв’язок, а саме

= ( Х'Х)^-1 Х'Y

Цей розв’язок називається оцінкою найменших квадратів вектора β.

Оцінку для β можна одержати й в інший спосіб.

ε'ε = (Y-Хβ)'(Y-Хβ) = Y'Y - 2β'Х'Y+ β'Х'Хβ