Дипломная работа: Статистичний аналіз тенденцій захворюваності в Україні

M[] = (X’X)^-1 X’M[Y] = (X’X)^-1 X’X β = β (1.1.9)

тобто є незміщеною оцінкою вектора β. Якщо, окрім того, припустити, що всi ε_i , і = 1, …, n - некорельовані і мають однакову дисперсію, тобто

соv[ε_i , ε_j ] = ,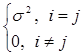

то D[ε] = σ² I_n ,

D[Y] = D[Y - Xβ] = D[ε], отже D[Y] = σ² I_n .

Звідси одержуємо

D[] = D[(Х'Х)^-1 Х'Y] = сov((Х'Х)^-1 X'Y, (Х'Х)^-1 X'Y) =

= (X'X)^-1 X'cov(Y,Y)((X'X)^-1 X')' = (X'X)^-1 X'DYX(X'X)^-1 =

= (X'X)^-1 X'σ² IX(X'X)^-1 = σ² (X'X)^-1 (X'X) (X'X)^-1 = σ² (X'X)^-1 (1.1.10)

Виникає таке питання: чому за оцінку вектора β ми вибираємо саме (оцінку найменших квадратів), а не будь – яку іншу оцінку? Далі покажемо, що в деякому розумному класі оцінок _j , є оцінкою параметра β_j з найменшою дисперсією. Цю оцінку _j можна „виділити" з вектора = (₀ , ₁ , ..., _{p -1} )' множенням зліва на вектор-рядок c', у якого (j +1)-й елемент рівний одиниці, а всі інші елементи дорівнюють нулю. Таку специфічну властивість оцінки _j , можна узагальнити на випадок довільної лінійної комбінації а'. Для цього використовуємо наступну теорему.

Теорема 1.1.4.

Нехай - оцінка найменших квадратів вектора = Хβ. Тоді в класі всіх лінійних незміщених оцінок лінійної комбінації c'θ оцінка c' є єдиною оцінкою, яка має мінімальну дисперсію. (Будемо говорити, що c' є найкращою лінійною незміщеною оцінкою (НЛНО) для c'θ)

Доведення.

Оцінку найменших квадратів вектора = Хβ представимо у вигляді

= X = X(Х'Х)^-1 X'Y = X(Х'Х)^-1 X'Y = PY,

при цьому

PX = X(Х'Х)^-1 X'X = X(Х'Х)^-1 X'X = XI = X .

Перевіримо, що c' - лінійна незміщена оцінка для c'θ. Дійсно,

M[c'] = Mc'РY = c'P MY = c'Pθ = c'PXβ = c'Xβ = c'θ

для всіх θΩ = [Х] і c' = c'PY = (P'c)'Y = (Рс)'Y. Розглянемо іншу лінійну незміщену оцінку для c'θ. Тоді M[d'Y] = c'θ з одного боку, а з іншого

M[d'Y] = d'MY = d'θ,

Тоді

c'θ = d'θ (с' - d')θ = 0 (с- d)'θ = 0, тобто (c - d) Ω = R(X).

Оскільки R(X) = R(P) в силу теореми 1.1.2, то

(c – d) R(P), (c – d)'P = 0 ((c – d)'P)' = 0' P(c – d) = 0

Pc = Pd

Порахуємо дисперсію оцінки c':

Dc' = D[(Рd)'Y] = D[(Рd)'Y] = Dd'P'Y = cov(d'P'Y, d'P'Y) =

= d'P'cov(Y, Y)(d'P')' = d'PDYPd = d'Pσ² IPd = σ² d'Р² d = σ² d'Рd,