Дипломная работа: Статистичний аналіз тенденцій захворюваності в Україні

(II) rank[I_n - Р] = tr[I_n - Р] = n - р.

(III) (I_n - Р)Х = 0.

Доведення.

(I) Р' = (X(X'X)^-1 X')' = X((X'X)^-1 )'X' = X(X'X)^-1 X' = P

Отже, матриця Р є симетричною і (I_n - Р)' = I_n - Р' = I_n - Р. Крім того,

Р² = X(Х'Х)^-1 Х'Х(Х'Х) ^-1 X' = XI_p (Х'Х)^-1 X' = Р,

і (I_n – Р)² = I_n - 2Р + P² = I_n – Р.

(II) Оскільки матриця I_n - Р симетрична та ідемпотентна, то вона проекційна і tr(I_n – Р) = rank(I_n – Р). Тоді

rank[I_n - Р] = tr[I_n - Р] = n - trР,

де

trР = tr[X (Х'Х)^-1 X'] = tr[Х'Х (Х'Х)^-1 ] = trI_p = р.

(III) (I_n - Р)Х = Х - Х(Х'Х)^-1 Х'Х = Х - Х = 0.

Теорема доведена.

Теорема 1.1.2.

Нехай Р = X(Х'Х)^-1 X', тоді R(P) = R(X), тобто простір, породжений стовпцями матриці P є простором, породженим стовпцями матриці Х.

Доведення.

R(P) = {z: z = Pα} для деякого α, R(X) = {Y: Y = Xγ} для деякого γ.

Вибираємо zR(P), тоді z = Pα. Отже,

z = Pα = X(X'X)^-1 X'α = Xβ,

отже zR(X).

Вибираємо YR(X), тоді Y = Xγ

Y = Xγ = X(X'X)^-1 X'Xγ = X(X'X)^-1 X'Xγ = PY,

отже YR(P).

Теорема доведена.

Теорема 1.1.3.

(Y - ) = 0 або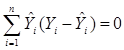

Доведення.

(Y - ) = { = X = X(X'X)^-1 X'Y = PY} = (PY)'(Y – PY) = Y'P'(1 – P)Y = = Y'P(1 – P)Y = Y'(P – P² )Y = Y'(P – P)Y = 0.

Теорема доведена.