Дипломная работа: Топологическая определяемость верхних полурешёток

Глава 2.

1. Верхние полурешётки.

Определение: Ч.у. множество называется верхней полурешёткой , если sup { a , b } существует для любых элементов a и b .

Определение: Непустое множество I верхней полурешётки L называется идеалом , если для любых включение имеет место тогда и только тогда, когда .

Определение : Верхняя полурешётка называется дистрибутивной , если неравенство ≤ (, , L) влечёт за собой существование элементов , таких, что , , и = .(рис.1). Заметим, что элементы и не обязательно единственны.

Некоторые простейшие свойства дистрибутивной верхней полурешётки даёт:

Лемма 1 :

(*). Если <, > - произвольная полурешётка, то верхняя полурешётка дистрибутивна тогда и только тогда, когда решётка дистрибутивна.

(**). Если верхняя полурешётка дистрибутивна, то для любых существует элемент , такой, что и . Следовательно, множество является решёткой.

(***). Верхняя полурешётка дистрибутивна тогда и только тогда, когда множество является дистрибутивной решёткой.

Доказательство.

(*). <, > - дистрибутивна и , то для элементов , , справедливо равенство :

значит, полурешётка <,> - дистрибутивна.

<,> - дистрибутивна. Пусть решётка содержит диамант или пентагон (рис.2).

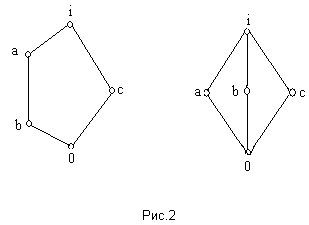
1) Пусть решётка содержит пентагон, . Нужно найти такие элементы и , чтобы выполнялось равенство . Но множество элементов меньших b или c состоит из элементов {0, b , c } и их нижняя граница не даст a . Получили противоречие с тем, что <,> - дистрибутивна. Значит, наше предположение неверно и решётка не содержит пентагона.

2) Пусть решётка содержит диамант, . Аналогично, множество элементов меньших b или c состоит из элементов {0, b , c }, их нижняя граница не даст a . Значит, решётка не содержит диаманта.

Можно сделать вывод, что решётка дистрибутивна.

(**). Имеем , поэтому , где (по определению дистрибутивной полурешётки). Кроме того, является нижней границей элементов и .

Рассмотрим идеалы, содержащие элемент и - и . Тогда Ø ,т.к. , нижняя граница элементов a и b , содержится там.

Покажем, что I ( L ) – решётка, т.е. существуют точные нижняя и верхняя грани для любых A и B .

Покажем, что совпадает с пересечением идеалов A и B . Во-первых, - идеал. Действительно, и и Во-вторых, пусть идеал и . Тогда , т.е. - точная нижняя грань идеалов A и B , т.е. .

Теперь покажем, что совпадает с пересечением всех идеалов , содержащих A и B . Обозначим . Поскольку для для , то C идеал. По определению C он будет наименьшим идеалом, содержащим A и B .

(***). Пусть – верхняя дистрибутивная полурешётка. Покажем, что

.