Дипломная работа: Целочисленные функции

ëx û — наибольшее целое, меньше или равное x ;

éx ù — наименьшее целое, больше или равное x .

Из определения ясно, что , . Отсюда следует, что

(1)

В целых точках неубывающие функции и совпадают, т.е. Û — целое Û. А если они не совпадают, то они отличаются на 1, т.е.

[- не целое] (2)

Эта формула связывает все три обозначения Айверсона. Здесь и далее квадратные скобки используются для произвольного высказывания P в таком смысле:

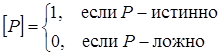
Функции и являются отображениями друг друга относительно координатных осей, т.е.

, (3)

Из определений «пола» и «потолка» легко следуют свойства этих функций: и

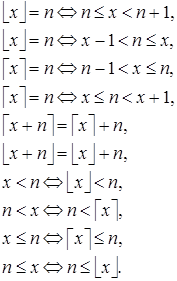(4)

Разность между и называется дробной частью x и обозначается

Иногда называется целой частью , поскольку .

Докажем следующее свойство рассматриваемых функций:

(5)

Так как равно либо 0, либо 1, то равно либо , либо .

II. Связь с непрерывными функциями.

Пусть — некоторая непрерывная монотонно возрастающая функция, обладающая тем свойством, что — целое число Þ — целое число. Тогда

(6)

и

(7)

всякий раз, когда определены функции,,.

Докажем, что

Случай 1: если , тогда .

Случай 2: если , тогда (в силу того, что функция монотонно возрастающая), а так как функция «пол» — не убывающая, то . Предположим, что , тогда существует такое число , что и (в силу непрерывности функции). Из условия следует, что — целое число. Это противоречит тому, что между и нет целых чисел. Значит, .

Докажем, что

Случай 1: если , то .

Случай 2: если , то (в силу того, что функция монотонно возрастающая), а так как функция «потолок» — не убывающая, то . Предположим, что , тогда существует такое число , что и (в силу непрерывности функции ). Из условия следует, что — целое число. Это противоречит тому, что между и нет целых чисел. Значит, .

Рассмотрев , получаем полезное свойство:

и (8)

Например, при и получаем , т.е. троекратное деление на 10 с последовательным отбрасыванием цифр остатка — это то же самое, что и непосредственное деление на 1000 с последующим отбрасыванием всего остатка.

III. Количество целых чисел в интервалах: [a, b], [a, b), (a,b), (a, b].

Будем рассматривать указанные интервалы при условии .

Если a и b — целые числа, тогда интервал [a , b ) содержит ровно целых чисел: a , a +1, …, , аналогично интервал (a , b ] содержит целых чисел, но a и b — произвольные вещественные числа. Из (4) следует

, когда — целое число

Поэтому интервал [a , b ) содержит ровно целых чисел, а интервал (a , b ] содержит ровно целых чисел.

Рассмотрим промежуток [a , b ]. Имеем (на основании свойств (4)). Отсюда следует, что рассматриваемый промежуток содержит ровно целых чисел: , , …, , .

Рассмотрим (a , b ), причём . Имеем . Отсюда следует, что рассматриваемый интервал содержит ровно целых чисел: , , …, , . Если не вводить дополнительное ограничение то получим, что пустой интервал (a , a ) содержит ровно целых чисел.

Подытожим установленные факты:

Интервал	Количество целых чисел	Ограничение
[a , b ]	ëb û-éa ù + 1	a £ b
[a , b )	éb ù-éa ù	a £ b
(a , b ]	ëb û-ëa û	a £ b
(a , b )	éb ù-ëa û-1	a < b

(9)