Дипломная работа: Целочисленные функции
Пусть α и β — вещественные положительные числа.
Докажем, что если Spec(α ) и Spec(β ) образуют разбиение всех целых положительных чисел, то α и β — иррациональные числа и 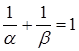 .
.
Spec(α ) и Spec(β ) образуют разбиение всех целых положительных чисел, тогда ![]() .
.
 Þ
Þ
Þ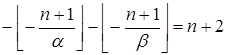 Þ
Þ
Þ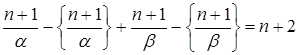 Þ
Þ
Þ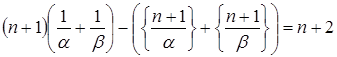 Þ
Þ
Þ![]()
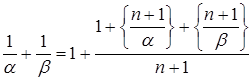
Рассмотрим 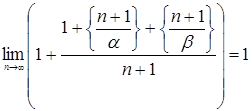 Þ
Þ
Þ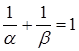 .
.
Докажем, что α и β иррациональны. Так как 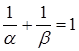 , то числа α и β либо оба рациональны, либо оба иррациональны.
, то числа α и β либо оба рациональны, либо оба иррациональны.
Если α и β оба рациональны, т.е. существует такое целое число m , что 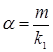 и
и 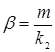 , где
, где ![]() и
и ![]() — натуральные числа, тогда
— натуральные числа, тогда ![]() ÎSpec(α ) и
ÎSpec(α ) и ![]() ÎSpec(β ).
ÎSpec(β ).
Но никакое число не содержится одновременно в двух спектрах, образующих разбиение всех целых положительных чисел. Следовательно, α и β — иррациональны.
Докажем обратное: если α и β иррациональны и 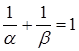 , то Spec(α ) и Spec(β ) образуют разбиение всех целых положительных чисел.
, то Spec(α ) и Spec(β ) образуют разбиение всех целых положительных чисел.
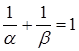 Þ
Þ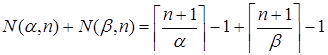
Так как ![]() и
и ![]() — иррациональны, то
— иррациональны, то ![]() и
и ![]() — не целые числа, то
— не целые числа, то
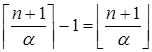
и
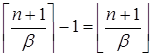
Отсюда получаем:
![]()
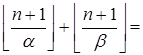
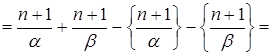
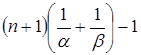 (так как
(так как 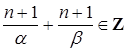 и
и ![]() и
и ![]() — иррациональны, то
— иррациональны, то 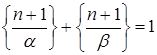 ).
).
Получаем, что![]() . Отсюда Spec(α ) и Spec(β ) образуют разбиение всех натуральных чисел.
. Отсюда Spec(α ) и Spec(β ) образуют разбиение всех натуральных чисел.
Что и требовалось доказать.
Задача 11.
Докажите, что ![]() при целом n .
при целом n .
Доказательство:
· если ![]() (
(![]() или
или ![]() ), то
), то ![]() ,
,
тогда![]() .
.
Получаем верное равенство ![]() .
.
· если ![]() , тогда
, тогда ![]() .
.
Правая часть имеет вид: 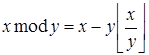 .
.
Преобразуем левую часть:
![]()
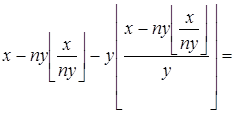
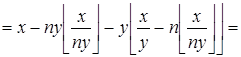
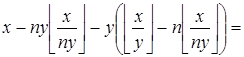
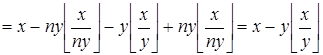 .
.