Дипломная работа: Целочисленные функции

Предположим, что каждый ящик содержит меньше, чем én / m ù предметов. Тогда наибольшее количество предметов в каждом ящике — это предметов. Следовательно, наибольшее количество предметов, размещённых по ящикам — это ÞÞ. Это противоречит тому, что .

Значит, существует ящик, который содержит не менее чем én / m ù предметов.

Предположим, что нет ящика, в котором не более, чем ën / m û предметов, т.е. каждый ящик содержит более чем ën / m û предметов. Тогда наименьшее количество предметов в каждом ящике — . Следовательно, наименьшее количество предметов, размещённых по ящикам — это ÞÞ. Это противоречит тому, что .

Значит, существует ящик, который содержит не более чем ën / m û предметов.

Что и требовалось доказать.

Задача 8.

Покажите, что выражение всегда равно либо ëx û, либо éx ù. При каких условиях получается тот или иной случай?

Решение:

1 случай: x = (4k - 1)/2, k ÎZ

Тогда , так как - целое число.

Получим ====

2 случай: x ¹ (4k -1)/2, k ÎZ, тогда .

Получим ==

Итак, данное выражение округляет числа до ближайшего целого; в случае «равновесия» — когда x лежит ровно посередине между целыми числами — данное выражение округляет число в сторону чётного.

Задача 9.

Докажите, что при любом целом n и любом целом положительном m .

Доказательство:

Пусть .

Покажем, что .

Имеем Û

Û (по свойствам (4)) Û

ÛÛ

ÛÛ

ÛÛ

ÛÛ

Û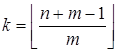

Что и требовалось доказать.

Задача 10.

Пусть α и β — вещественные положительные числа. Докажите, что Spec(α ) и Spec(β ) образуют разбиение всех целых положительных чисел тогда и только тогда, когда α и β иррациональны и 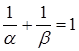.