Дипломная работа: Целочисленные функции
Ответ: b — целое число.
Задача 15.
Найдите сумму всех чисел, кратных x , в замкнутом интервале [a , b ], при ![]() .
.
Решение:
Числа, кратные ![]() имеют вид
имеют вид ![]() , где
, где ![]() . Нужно просуммировать те из чисел
. Нужно просуммировать те из чисел ![]() , для которых
, для которых ![]() . Учитывая, что
. Учитывая, что ![]() и (4), имеем
и (4), имеем
![]() Û
Û![]() Û
Û .
.
Нам нужно вычислить следующую сумму:
 .
.
В этой сумме ![]() можно вынести за скобки, а в скобке останется сумма всех чисел от
можно вынести за скобки, а в скобке останется сумма всех чисел от ![]() до
до ![]() включительно. Применяя формулу арифметической прогрессии получаем:
включительно. Применяя формулу арифметической прогрессии получаем:
 .
.
Задача 16.
Покажите, что n -й член последовательности 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,… равен![]() . (Каждое число m входит в данную последовательность m раз.)
. (Каждое число m входит в данную последовательность m раз.)
Решение:
В этой последовательности чисел меньших ![]() будет
будет ![]() , а чисел не превосходящих
, а чисел не превосходящих ![]() будет
будет ![]() . Поэтому, если xn = m , то
. Поэтому, если xn = m , то
Оценим n :
![]() Û
Û
Û![]() Û
Û
Û![]() Û
Û
Û![]() Û
Û
Û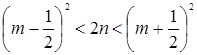 Û
Û
Û![]() Û
Û
Û![]() Þ
Þ
Þ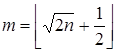 .
.
Следовательно, 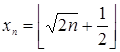 .
.
Задача 1 7 .
Найдите и докажите связь между мультимножествами Spec(α ) и Spec(α /(α +1)), где α — некоторое положительное вещественное число.
Решение:
Число элементов в Spec(α ), которые не превосходят n :
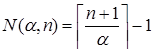 .
.
Число элементов в Spec(α /(α +1)), которые не превосходят n :
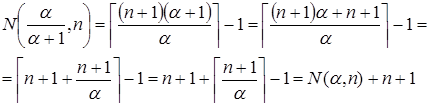 .
.
Итак, получили, что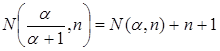 .
.
Покажем на основе этого, что чисел равных ![]() в Spec
в Spec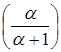 будет на 1 больше, чем в Spec(
будет на 1 больше, чем в Spec(![]() ).
).
При ![]() если
если ![]() , тогда
, тогда 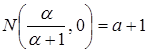 .
.
Пусть в Spec(![]() ) элементов не превосходящих
) элементов не превосходящих ![]() будет
будет ![]() , тогда число элементов в Spec(
, тогда число элементов в Spec(![]() ) равных
) равных ![]() будет
будет ![]() . Подсчитаем количество элементов в Spec
. Подсчитаем количество элементов в Spec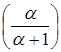 равных
равных ![]() :
: